角の２等分線の性質 　 　　　　　　　 　　　　　　　　　　　　　　　

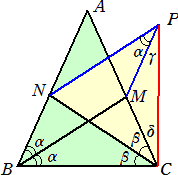
　∠Ａ＝４０°の△ＡＢＣにおいて、∠Ｂ、∠Ｃの２等分線が辺ＡＣ、ＡＢとそれぞれＭ、Ｎで交
わるとする。ＢＭ＝ＣＮのとき、∠Ｂ、∠Ｃの大きさをそれぞれ求めよ。









































（答）　∠Ｂ＝∠Ｃ＝７０°

（コメント）　有名問題らしいです．．．。


　DD++さんからのコメントです。（平成２７年１１月２１日付け）

　手間はかかりますが、さほど難しい問題というわけでもないですね。40°が特別意味を持
つわけでもないので、三角比と因数分解の面倒な計算を処理する練習といった印象。

　BC=a、CA=b、AB=c とします。△ＡＢＣの面積を考えて、

　　(1/2) (a+c) BM sin(B/2) = (1/2) (a+b) CN sin(C/2)

　両辺を BM=CN で割り、2乗して8倍すると、

　　(a+c)²・2sin² (B/2) = (a+b)²・2sin² (C/2)

　半角の公式を用いて、　(a+c)²(1-cosB) = (a+b)²(1-cosC)

　余弦定理を用いて、両辺に 2abc をかけると、

　　b (a+c)²(2ac-a²-c²+b²) = c (a+b)²(2ab-a²-b²+c²)

　これが b と c について交代的であることと、形式的に a=b+c のとき明らかに両辺 0 になる
ことに注意すると、交代式の性質と因数定理を用いて、この五次方程式は容易に以下のよう
に変形できます。

　(b-c) (a-b-c) {a³+a²(b+c)+3abc+bc(b+c)} = 0

　これは、a＞0、b＞0、c＞0、a＜b+c という条件では、b=c 以外に解はありません。

　よって、これは頂角40°の二等辺三角形であることが示されたので、 B=C=70° です。


（コメント）　DD++さん、ありがとうございます。今日（１１月２１日）、筑波大学附属駒場高校
　　　　　　で、確率の授業を聞きながら、次の事実の証明を考えていました。

　　△ＡＢＣにおいて、∠Ｂ、∠Ｃの２等分線が辺ＡＣ、ＡＢとそれぞれＭ、Ｎで交わり、
　ＢＭ＝ＣＮのとき、△ＡＢＣは、ＡＢ＝ＡＣの２等辺三角形である。

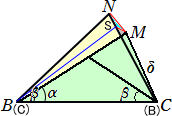
　幾何学的な証明が出来ないものかと考えていましたが、難しいですね！結局、次のような
証明をでっち上げてみました。どうなんでしょうか？

左図のように、点Ｐを四角形ＢＭＰＮが平行四辺形になるよ 　　うにとる。 　　　題意より、ＮＣ＝ＮＰ　で、α＋γ＝β＋δ　が成り立つ。 　　今、β＞α　と仮定すると、ＢＮ＝ＭＰ＞ＣＭ　より、δ＞γ 　　このとき、α＋γ＝β＋δ　より、　α＞β　で、矛盾。 　　β＜α　としても同様に矛盾が示される。

　以上から、α＝βが成り立ち、△ＡＢＣはＡＢ＝ＡＣの２等辺三角形である。


（コメント）　何となくスッキリしない証明です。もっとスカッとする証明はないでしょうか？

　上記の証明でスッキリしない部分は、「β＞α　と仮定すると、ＢＮ＞ＣＭ」という推論である。

　この論点に関して、次のように証明され推論が正しいことが確認される。自己解決で、ちょ
っとスッキリかな！

（証明）　△ＢＣＮを裏返して、△ＢＣＮに下図のように重ねる。

　　　　

　β＞α　とする。∠ＮＢＭの２等分線がＣＮと交わる点をＳとおく。

　このとき、△ＢＭＳ≡△ＢＮＳ　なので、ＳＭ＝ＳＮ　となり、△ＳＭＮは２等辺三角形である。

　よって、　∠ＭＮＣ＝∠ＮＭＳ＜∠ＮＭＣ　より、　ＣＭ＜ＢＮ　　（証終）


　DD++さんのように余弦定理を用いて計算してみました。

　ＡＭ＝ｂｃ/（ｃ＋ａ）、ＡＮ＝ｂｃ/（ａ＋ｂ）　なので、

　ＢＭ²＝ｃ²＋（ｂｃ/（ｃ＋ａ））²−２ｃ・（ｂｃ/（ｃ＋ａ））ｃｏｓ４０°

　ＣＮ²＝ｂ²＋（ｂｃ/（ａ＋ｂ））²−２ｂ・（ｂｃ/（ａ＋ｂ））ｃｏｓ４０°

　ここで、ＢＭ＝ＣＮ　で、ｃｏｓ４０°＝（ｂ²＋ｃ²−ａ²）/(２ｂｃ）　を代入して整理すると、

（ｂ−ｃ）（ａ⁵＋２ａ⁴（ｂ＋ｃ）＋ａ³（ｂ²＋５ｂｃ＋ｃ²）＋４ａ²ｂｃ（ｂ＋ｃ）＋ａｂｃ（ｂ＋ｃ）²）＝０

　よって、ｂ＝ｃ　から、△ＡＢＣはＡＢ＝ＡＣの２等辺三角形である。