
当HPがいつもお世話になっているHN「GAI」さんからの出題です。
(平成27年5月17日付け)
鋭角三角形ABCの外接円の中心をOとし、線分OA、BCの中点をそれぞれM、Nとする。
このとき、∠OMN=θで、∠B=4θ、∠C=6θ であるなら、θは何度か?
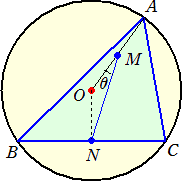
また、θを度数法で表すとき、∠B、∠Cがθの整数倍で、θが整数と成り得る場合の∠B、
∠Cの角度の組合せを全て求めて下さい。ただし、 0°<θ<90°とする。
(答) DD++さんが考察されました。(平成27年5月17日付け)
∠ABC=∠ACB-2θ より、∠ABO=∠ACO-2θ つまり、∠BAO=∠CAO-2θ
したがって、弧BC(Aを含まない側)の中心をPとすると、APは∠BACの二等分線なのだか
ら、 ∠OAP=θ となる。
したがって、∠OAP=∠OMN で、同位角が等しいので、MN//AP
そして、3点O、N、Pは一直線上にあり、OM=MA なので、ON=NP=OB/2
すなわち、 ∠BON=∠CON=60°で、∠BAC=180°-10θ=60° より、 θ=12°
同様にすると、∠Bと∠Cは差が2θのとき、和が120°になるわけですから、nを3以上の
60の正約数として、∠B=(n-1)θ、∠C=(n+1)θ と設定すれば、θ=(60/n)° と10通りが求ま
りますが、それで全てかと言われるとこのアプローチでは無理そうですね。
GAI さんからのコメントです。(平成27年5月18日付け)
意図としては、この10パターンを探り出すことを意識していたんですが、表現が足らずに他
からの構造(二等辺三角形によらない。)も有り得ると出題した後気付いてしまいました。でも
どうやったら探し出せるのかは分かりませんでした。
らすかるさんからのコメントです。(平成27年5月18日付け)
条件を満たすものは、10通り以外に、以下の7通りがあるようです。(ただし、∠B<∠C)
(θ,∠B,∠C)=(1,30,61)、(2,30,62)、(3,30,63)、(5,30,65)、(6,30,66)、(10,30,70)、(15,30,75)
DD++さんからのコメントです。(平成27年5月18日付け)
∠Bと∠Cの差が2θ以外でもやっぱりできるのか……。
GAI さんからのコメントです。(平成27年5月18日付け)
(2,60,64)、(6,60,72)、(10,60,80) は構成できませんかね?もし、これが作れるならサイクリッ
ク的に、とってもバランスがとれるんですけど・・・。分度器と定規で作図していますが、誤差が
出るので確証が取れません。もし計算上で確認できたら調べて下さい。
らすかるさんからのコメントです。(平成27年5月19日付け)
∠B=60、∠C=64 のとき、 θ=2.1118151026°
∠B=60、∠C=72 のとき、 θ=6.8711010976°
∠B=60、∠C=80 のとき、 θ=12.1220128557°
なのでダメですね。
DD++さんからのコメントです。(平成27年5月20日付け)
sinα° + sinβ° + sinγ° = 0
これを満たす180の倍数でない整数 α、β、γ は、それらの角度に対応する単位円上の
点が、「正三角形の頂点またはそれらのいくつかをy軸対称なところに移動させたもの」に限
るか?
これが真だと示されれば、それらがθと-2B-θと2C-θに対応するとして、倍数関係を満
たすものをピックアップして全解が出る、ということまでわかりました。
しかし、これがなかなか証明できません。どなたかいいアイデアお持ちでないでしょうか。
らすかるさんからのコメントです。(平成27年5月20日付け)
限らないようです。(α,β,γ)=(18,30,234)とこれを180°回転した(α,β,γ)=(54,198,210)
そして、このうちのいくつかをy軸対称に移動したものが反例になっています。
DD++さんからのコメントです。(平成27年5月20日付け)
なるほど、つまり倍数関係を満たさないからたまたま候補に上がってこなかっただけで、他
にもあるんですね。となると、このアプローチの未来は明るくなさそうですか。