
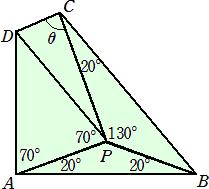
丂巐妏宍俙俛俠俢偺撪晹偵揰俹偑偁傝丄
丂丂丂佢俹俙俛亖佢俹俛俙亖佢俹俠俛亖俀侽亱丄佢俢俙俹亖佢俢俹俙亖俈侽亱丄佢俛俹俠亖侾俁侽亱
傪枮偨偡偲偒丄佢俢俠俹偺戝偒偝傪媮傔傛丅
乮嶲峫丗拀攇戝妛晬懏嬵応崅峑悢妛壢妛尋媶夛曇丂乽俠倎倖倕丂俛倧倢倢倵倕們倠丂俶倧丏嘮乿乯
丂丂丂丂丂丂
乮摎乯丂佢俢俠俹亖俉侽亱偲側傞丅
丂丂丂丂丂丂
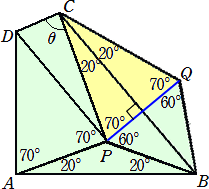
丂忋恾偺傛偆偵丄仮俛俹俠傪曈俛俠偵娭偟偰懳徧堏摦偝偣偨仮俛俻俠傪曈俛俠偵増偭偰揬傝崌傢
偣傞丅
丂偙偺偲偒丄俹俻佦俛俠偱丄仮俠俹俻偼掙妏偑俈侽亱偺俀摍曈嶰妏宍偲側傞丅
丂傛偭偰丄丂仮俢俙俹佭仮俠俹俻丂傛傝丄俹俠亖俹俢丂偱丄仮俹俠俢偼俀摍曈嶰妏宍偲側傞丅
丂佢俙俹俛亖侾係侽亱側偺偱丄佢俠俹俢亖俀侽亱
丂偟偨偑偭偰丄丂兤亖乮侾俉侽亱亅俀侽亱乯/俀亖俉侽亱
乮捛婰乯丂暯惉俀俇擭侾寧俀俇擔晅偗
丂忋婰偺夝摎偱梡偄傜傟偨庤朄偼丄庴尡悢妛偱偼偍撻愼傒偺傕偺偩傠偆丅俀侽侾俁擭搙擖帋
搶嫗戝妛慜婜棟宯丂戞係栤偵師偺傛偆側栤戣偑弌戣偝傟偨丅
丂仮俙俛俠偵偍偄偰丄佢俛俙俠亖俋侽亱丄乥俙俛乥亖侾丄乥俙俠乥亖
偺揰偑丄俹俙/乥俹俙乥亄俹俛/乥俹俛乥亄俹俠/乥俹俠乥亖侽丂傪枮偨偡偲偡傞丅
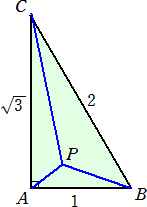
乮侾乯丂佢俙俹俛丄佢俙俹俠丂傪媮傔傛丅
乮俀乯丂乥俹俙乥丄乥俹俛乥丄乥俹俠乥丂傪媮傔傛丅
乮摎偊乯丂乮侾乯丂壗傟傕丂侾俀侽亱乮俀乯丂乥俹俙乥亖侾/
丂乮侾乯偵偮偄偰丄倎亖俹俙/乥俹俙乥丄倐亖俹俛/乥俹俛乥丄們亖俹俠/乥俹俠乥丂偲偍偗偽丄偙傟傜偼
扨埵儀僋僩儖偲側傝丄傑偨丄忦審傛傝丄倎亄倐亄們亖侽丂偑惉傝棫偮丅偙傟傜偺忦審偱丄倎 偲 倐丄
倎 偲 們 偺側偡妏傪媮傔傞栤戣偼嫵壢彂偺椺戣儗儀儖偱丄庴尡惗偵偲偭偰偼昁偢姰摎偡傋偒
栤戣偩傠偆丅
丂乮俀乯偵偮偄偰丄挌擩偵惓尫掕棟丄梋尫掕棟丄嶰妏娭悢偺憡屳娭學丄壛朄掕棟傪揔梡偡傟
偽夝偗傞偙偲偼夝偗傞偑丄偦傟傎偳梕堈偄偲偼巚傢傟側偄丅偙傟偵懳偟丄忋婰偺夝摎偺庤
朄乮崌摨側恾宍傪慄懳徧堏摦乯乯傪梡偄傟偽丄偦傟傎偳嬄乆偟偄寁嶼傪偟側偔偰傕梕堈偵夝
偐傟傞偙偲偵婥偯偐偝傟傞丅偨偩丄偙偺傾僀僨傾傪庴尡応偱惗傒偩偡偺偼尩偟偄偐傕丏丏丏丅
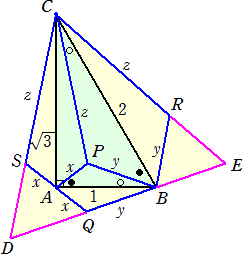
丂丂嵍恾偵偍偄偰丄仮俼俛俤丄仮俠俢俤丄仮俽俢俻偑惓嶰
丂妏宍偵側傞偙偲偼柧傜偐偩傠偆丅
丂丂捈偪偵丄倸亄俀倶亖俀倶亄俀倷亖倷亄倸丂偡側傢偪丄
丂丂丂倷亖俀倶丂丄丂倸亖俀倷亖係倶丂丂偑摼傜傟傞丅
丂丂梋尫掕棟偐傜丄丂倶2亄倷2亄倶倷亖侾
丂丂丂丂丂丂丂丂倷2亄倸2亄倷倸亖係丂丄丂倸2亄倶2亄倸倶亖俁
丂側偺偱丄倷亖俀倶丄倸亖係倶丂傪戙擖偡傟偽丄摎偊偼偡偖
丂媮傔傜傟傞丅
乮僐儊儞僩乯丂惓嶰妏宍傪梡偄傞曽朄埲奜偵丄仮俙俛俹佷仮俛俠俹傪梡偄偰傕傛偄丅忋恾傛傝丄
丂丂丂丂丂丂憡帡斾偑 侾丗俀 側偺偱丄倷亖俀倶丄倸亖俀倷亖係倶丂偼捈偪偵摼傜傟傞丅偙偪傜偺曽偑
丂丂丂丂丂丂傛傝娙柧偐傕偟傟側偄丅