
次の△ABCにおいて、点Mは辺BCの中点で、∠BAM=30°、∠B=15°とする。
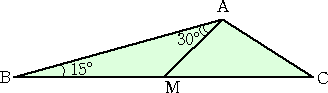
このとき、∠Cは何度だろうか?
(答) 30度
次のような鮮やかな補助線の存在に驚かされる。
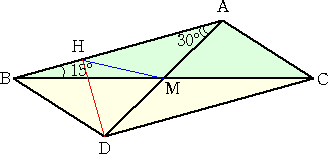
AM=DMとなる点Dを直線AM上にとり平行四辺形ABDCを作る。点Dより辺ABに垂線
DHを引く。∠ADH=60°と DM=DH から△DMHは正三角形となる。
よって、MA=MHから∠MHA=30°で、∠HMB=15°となる。
すなわち、△HBMは二等辺三角形で、BH=MH となる。
よって、△DHBにおいて、∠DHB=90°で、HB=HD から、∠HBD=45°となる。
このとき、∠DBC=30°で、平行線における錯角は等しいから、
∠BCA=∠DBC=30°
となる。
(参考文献:田村三郎 著 数学パズルランド (講談社))
DD++さんからのコメントです。(平成28年10月8日付け)
掲載されている補助線も見事ですが、こっちの方が地に足ついた解法かな、と。
点Bから線分AMに下ろした垂線の足をHとする。BH=1とすると、BM=
なので、2辺の比と間の角相等より、 △BMA∽△BAC。 よって、∠BCA=∠BAM=30°
(コメント) なるほど!DD++さんの解答の方が自然ですね。感動しました。