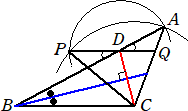
∠PDB=180°−2(90°−●)=2●
よって、 PD‖BC
∠B>90°である三角形ABCがある。いま辺AB上の点Dと点Cを折り目として頂点Aが移っ
た点をPとしてBC‖PDとなるようにしたい。
三角形ABCと同じ面積を持つこの条件を満たす境界をとるためには点Dはどこにとればよ
いか?
らすかるさんからのコメントです。(平成30年4月6日付け)
「辺AB上の点Dと点Cを折り目として」というのは「辺AB上の点Dと点Cを通る直線に関して
対称移動することにより」という意味でしょうか。
三角形ABCと同じ面積を持つこの条件を満たす境界をとるためには点Dはどこにとればよ
いか?
私の国語力が貧弱なせいか、この文は何度読んでもわかりませんでした。「三角形ABCと
同じ面積を持つ」が何にかかるのかわからず、「境界をとる」の意味もわかりませんでした。
あとタイトルの「境界線の引き直し」とのつながりもわかりませんでした。
GAI さんからのコメントです。(平成30年4月7日付け)
色々書き過ぎてすみません。改めて、
三角形ABCで辺AB上に点Dをとる。(ただし∠C>90°の鈍角三角形とする。)線分DCで
三角形を折り返し頂点Aが移る点をPとする。
[1] PD‖BC [2] PD⊥BC
がそれぞれ起こるようにするには点Dをどこに選べばよいか?
らすかるさんからのコメントです。(平成30年4月7日付け)
それであれば、
[1] Cを通り、∠Bの二等分線と直交する直線とABの交点をDとすればよい。実際に、
 |
∠BDC=∠QDC=90°−● なので、 ∠PDB=180°−2(90°−●)=2● よって、 PD‖BC |
[2] Cを通り、∠Bの二等分線と45°の角度をなす直線とABの交点をDとすればよい。
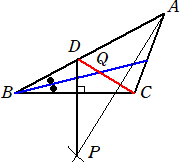 |
実際に、∠BCD+2●=∠ADC=45°+● なので、 ∠BCD=45°−● 、∠PDC=45°+● よって、 PD⊥BC |
[2]は、∠C>∠A+90°の場合、すなわち、Cを通り、BCに直交する直線とABの交点をEと
したときにAE>CEとなる場合は2点あります。
GAI さんからのコメントです。(平成30年4月7日付け)
これは、実験しながら思いついた問題でした。
[1]は、BCの長さをBよりAB上にとった点をDとすれば上手くいくと感じた。
(結局らすかるさんが示された事に同じでした。)
[2]は、最初計算でごりごり進めていたんですが、先に行くにつれ、どえらく複雑な式に膨ら
んでいき、収集がつかなくなりました。
紙でいろいろ折り返して観察していたら、ABへCから垂線を引き交点をHとする。CHの長さ
をCからBC上に移しその点をH'とする。H'にBCの垂線を立てABとの交点をDとすると、上手
くいくとの感触を持てた。
らすかるさんのコメントにあるように、場合によればもう一点存在するとは思ってもいませ
んでした。
