四角形ABCDの面積は四角形ABDCの面積の２倍 ⇔ f(s，t)＝０ である。
これを満たす二変数関数 f(x，y) を一つ求めよ。
ただし、f(x，y) は場合分けなどせず、一つの式でなければならない。
（コメント） 題意を満たす絵を描いてみると、下図のようになる。
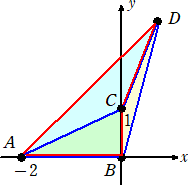△ＡＣＤ＝ｔ−ｓ/２−１ より、四角形ABCDの面積＝ｔ−ｓ/２また、四角形ABDCの面積＝ｓ/２＋１ なので、
ｔ−ｓ/２＝２（ｓ/２＋１） より、 ｔ−３ｓ/２−２＝０
よって、 f(s，t)＝ｔ−３ｓ/２−２ （ただし、ｓ≧０、ｔ≧１）
DD++さんからのコメントです。（平成３０年２月１０日付け）
場合分け「など」ということは、単純に定義域をつけるもの、例えば、x+y=1 (0<x<1) のよう
なものもダメってことですかね？
らすかるさんからのコメントです。（平成３０年２月１０日付け）
はい、その通りです。
（コメント） ということは、上記の（コメント）の解は「ボツ」ですね！
りらひいさんからのコメントです。（平成３０年２月１０日付け）
定義される範囲を無理やりくっつけた、こんな感じの式はありなのかな？
h(x，y)=3x-1+5/(1+y^2) 、g(x，y)=exp(ln(h(x，y)))-h(x，y) として、
f(x，y)=(x+2y+4)(3x-2y+4)+g(x，y)
らすかるさんからのコメントです。（平成３０年２月１０日付け）
式の形としてはOKですが、答えがちょっと違います。
DD++さんからのコメントです。（平成３０年２月１１日付け）
じゃあ、極限関数でも使いましょう。
f(x，y) = lim[z->∞] {(x+2y+4)(3x-2y+4)+e^{xy(x-2y+2)z}}
でいかがでしょうか。
＃……と思ったら変なところに孤立点ができますね、これ。もう一捻り必要か。
冷静に考えれば、正であることを一度に保証しなくても、負と0を別々の方法で排除すれば
いいだけですね。
f(x，y) = (x+2y+4)(3x-2y+4)/√{xy(x-2y+2)}
でどうですかね。
らすかるさんからのコメントです。（平成３０年２月１１日付け）
正解・・・だと思ったらちょっと違いますね。排除する側が反対です。用意していた解答は考
え方は全く同じで、√の中身をxy(2y-x-2)にしたものです。
# さらに、「f(x，y)は実数全体で定義される」という条件も付けたかったのですが、これは難し
いですね。DD++さんのアイデアを使うと、
f(x，y) = lim[z->∞] {(x+2y+4)(3x-2y+4)+ze^{xy(x-2y+2)z}}
とはできますが、もう少し綺麗な式が作れないかな、と思います。
DD++さんからのコメントです。（平成３０年２月１１日付け）
あっ。極限関数のときには最終的に正の方を排除する形にしたの忘れてました。
（コメント） DD++さん、らすかるさんの解をGrapesで描いてみました。いろいろなところに
Ｄの存在可能性があるんですね。驚きました。
