点Oから平面ABCに下ろした垂線の足Hが三角形ABCの外心であることを示せ。
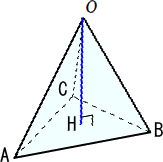
答えを入手できない問題で、苦戦しております……。
りらひいさんからのコメントです。(平成29年10月13日付け)
AH⊥OHより、 |AH|^2=|OA|^2-|OH|^2
BH⊥OHより、 |BH|^2=|OB|^2-|OH|^2
CH⊥OHより、 |CH|^2=|OC|^2-|OH|^2
|OA|=|OB|=|OC| なので、 |AH|^2=|BH|^2=|CH|^2
|AH|>0、|BH|>0、|CH|>0 なので、 |AH|=|BH|=|CH|
よって、点Hは三角形ABCの外心である。
# ベクトルの要素を全然使わなかった・・・。
(コメント) 可能性は、いくつかある小問のうちの1問なのでは...?
Gentaさんからのコメントです。(平成29年10月13日付け)
丁寧な解答、ありがとうございました...m(__)m。
