正方格子を縦にａ個、横にｂ個並べた長方形を考えます。左上から４５°の角度で進
みヘリに着くと、反射することを繰り返す時、どの角に来るか
例えば、ａ＝３、ｂ＝５ のとき、下図のように、Aを出発しＣに至る。
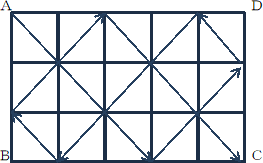
（考察１）
縦＝奇数、横＝奇数のとき、Ｃ右下が終着点となる。
縦＝偶数、横＝奇数のとき、Ｂ左下が終着点となる。
縦＝奇数、横＝偶数のとき、Ｄ右上が終着点となる。
（考察２）
縦、横が互いに素ならば、全ての格子を通る。
（考察３）
下に１個右に２個進む場合はどうなるでしょうか。
（考察４）
長方形の格子の場合はどうなるでしょうか。
（考察５）
縦横が公約数ｎを持つとき、格子全体のｎ分の１を通る。
このたび、直方体に拡張した問題に出会いました。何と、
とπとｅの長さを縦横高さにもつ直方体を面にそって経路をたどると、元の頂点に戻る
とありました。本当でしょうか？
直方体のときは、始発の頂点から、どういう条件で他の頂点に移るのでしょうか？
縦１、横
の長方形で、４５°の角度で経路をくりかえすとき、どの角にも、こないことの証明をお願いします。
らすかるさんからのコメントです。（平成２９年１０月６日付け）
角に到達した時、それまでの縦方向と横方向の移動距離が同じ(45°なので)ですが、縦
方向の移動距離は、ｍ(有理数)、横方向の移動距離は、ｎ
(無理数)なので、同じになることはありません。
ｋｓさんからのコメントです。（平成２９年１０月６日付け）
らすかるさん、ありがとうございます。
縦＝無理数、横＝無理数（横の整数倍でない）ときは、どうなりますか？
らすかるさんからのコメントです。（平成２９年１０月６日付け）
縦横比が有理数であれば、角に到達します。例えば、
縦=
、横=
ならば到達せず、縦=2π、横=3πならば到達します。ｋｓさんからのコメントです。（平成２９年１０月６日付け）
すみません。同じ理屈ですよね。ところが、空間のときは、
とeとπで直方体を考えると、始発の頂点に戻ってくることが不思議です。縦＜横＜高さのとき、縦＋横＝高さ+αがなり
たつとき、戻ってくるようです。
DD++さんからのコメントです。（平成２９年１０月６日付け）
自分が反射するんじゃなく、長方形の方を反転させて隣に新しく作っていくと考えてみてくだ
さい。反射の場合は長方形格子になるので比が無理数だとどうしようもありませんが、直方
体表面をなぞる場合はそうならず、最も長い辺を含む面内から出発すると、著しく偏った直
方体でない限り、４回辺を通った後で元の頂点に戻ることは明らかだと思います。
ｋｓさんからのコメントです。（平成２９年１０月１０日付け）
長方形の場合は反射があり偶奇性が関係していますが、直方体の場合は、それがなく、
完全に別問題ですよね。同じ流れで本に書かれてあって、勘違いしました。不思議さもない
ですね。
