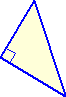
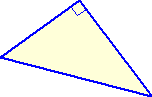
伸び縮みする素材に図形を描いて、一定方向に伸ばすと図形の形が変わる、そんな体験
からの問題です。(投稿888回記念)
問題 xy平面上に、各辺が座標軸に平行でない直角二等辺三角形がある。この直角二等
辺三角形をx軸方向にa倍に拡大すると、また、直角二等辺三角形になるという。定数
aの値を求めよ。
 |
横方向に引き伸ばすと、 |  |
解法はいくつか考えられる。
(解1) 座標平面で、A(1,m)、B(m,−1)、O(0,0)とし、∠AOB=90°なる直角二等
辺三角形AOBを考える。ただし、m>0 とする。
この図形をx軸方向にa倍に拡大して、A’O=A’B’、∠OA’B’=90°なる直角二等辺三
角形A’OB’になるものとする。
A’(a,m)、B’(am,−1)なので、 ベクトルOA’=(a,m)、OB’=(am,−1) より、
A’B’=(a(m−1),−m−1)
条件より、 A’O=A’B 、A’O⊥A’B’ なので、
a2+m2=a2(m−1)2+(m+1)2 すなわち、 a2(m2−2m)+2m+1=0
また、 a2(m−1)−m2−m=0
これより、a2を消去すると、 (m2−2m)(m2+m)+(2m+1)(m−1)=0
すなわち、 m4−m3−m−1=0 から、 (m2+1)(m2−m−1)=0
mは実数で、m>0 なので、 m=(1+![]() )/2 となる。
)/2 となる。
このとき、 a2=(m2+m)/(m−1)=(2m+1)/(m−1)=(7+3![]() )/2 より、
)/2 より、
a=√{(14+2√45/4}=(3+![]() )/2 (終)
)/2 (終)
(解2) 直角2等辺三角形の直角を挟む2辺を斜辺とする2つの直角三角形が合同になる
という性質がある。
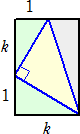 |
横方向に引き伸ばすと、 | 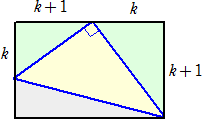 |
横方向にa倍(ただし、a>1)に拡大したので、 a=k+1 、ak=2k+1 が成り立つ。
kを消去して、 a(a−1)=2(a−1)+1 すなわち、 a2−3a+1=0
よって、 a=(3+![]() )/2 (終)
)/2 (終)
(コメント) 図形の性質に着目した(解2)が一番初等的かな?
(解3) 元の図形と横に引き伸ばした図形から、次のような立体図形を考えることが出来る。
ちょうど、元の図形を底面とする三角柱を平面で切断したような図形である。
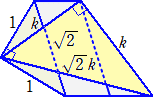
横方向にa倍(ただし、a>1)に拡大すると、面積比はk2倍になるので、 a=k2 である。
このとき、 √(k2−2)+√(k2−1)=√(2k2−1)
すなわち、 √(a−2)+√(a−1)=√(2a−1)
両辺を平方して、2a−3+2√(a−2)√(a−1)=2a−1 から、√{(a−2)(a−1)}=1
よって、 a2−3a+1=0 より、 a=(3+![]() )/2 (終)
)/2 (終)
(コメント) 立体図形をイメージするというのは新鮮な発想ですね!
