あり、それぞれは17π（cm3)、23π（cm3)の容積が量れるとする。
このとき、水をちょうど100(cm3)量りとるにはどうすればよいか？
(100πではないことに注意！）
カルピスさんからのコメントです。（平成２９年８月１８日付け）
(1) １７πで３回捨てる
(2) ２３πで３回捨てる
(3) ２３πを満たしてから１７πに移すと６π残る
(4) １７πを円柱に戻し、上記の６πを捨てる
(5) (4)の操作を５回繰り返すと、１００立法ｃｍが円柱に残る
たぶん、おそらく、間違っているなぁ～。
（コメント） 操作(5)がよく分からないですね？
17π（cm3)、23π（cm3)の容積の線形結合では絶対に有理数は作れないので、２つのビ
ーカーはフェイクと判断しました。下図のように円柱を傾ければ、残った水の量が100(cm3)
となります。
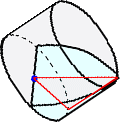実際に、左図の水の体積は、Ｖ＝∫-55 （１/２）（６/５）√（２５－ｘ2）√（２５－ｘ2）ｄｘ
＝（６/５）∫05 （２５－ｘ2）ｄｘ＝１００(cm3)
ＧＡＩ さんからのコメントです。（平成２９年８月１８日付け）
この余計なπをどうのけるかが難点。このビーカーを使う限りそれから逃れられない。ここ
は、このビーカーをダミーとして見破ることが重要。もともと容器に入っている水の体積は、
5^2*π*6=150*πで、これを100にするには、150*π-100の水を捨てればよい。
それは、元の体積の (150*π-100)/(150*π)=0.7877934092･･･≒0.7878=26/33 で、
約26/33も捨てないといけない。
更に甘く見積もっても、 0.75=3/4 だから、ビーカーを用いず、3/4以上を捨てるには元の
容器の半分の更に半分を捨ててもよい。
こうして考えられる捨て方が、容器を傾けていきながら上部から水を溢れさせ水面が容器
の底面が見え出すまでまず傾けていく。これでまず1/2を捨て去る。
さて、残った水をさらに半分近く捨て去る手は水面が底面の直径になるまでさらに傾ける
という方法は？（あくまで想像）
そこで、計算による確認。
もし容器を傾けていき水面が底面の直径部分に一致したときの残った容器内の水の体積
を考えてみると、一般に半径がa、高さがhの円柱容器であるとき、求める体積は底面の直径
部分をx軸にとり、底面の中心（原点）から t だけ離れた部分での残り水の形状を底面に垂
直に切断した断面積S(t)は直角三角形で、その直角を挟む２辺の長さは、
√(a^2-t^2)とh/a*√(a^2-t^2) (∵底面と水面がなす角θはtanθ=h/aだから)
よって、 S(t)=1/2*√(a^2-t^2)*h/a*√(a^2-t^2)=h/(2*a)*(a^2-t^2)
これより残っている水の体積Vは、
Ｖ
=2*∫[0,a]S(t)dt
=2*h/(2*a)[F(a)-F(0)](ただしF(t)=a^2*t-t^3/3)
=2/3*h*a^2
（これは正に元の体積a^2*π*hの1-2/3*h*a^2/(a^2*π*h)=1-2/(3*π)=0.7877934092･･･を
捨て去ったことに一致している。）
本題は、a=5、h=6であるので、V=2/3*6*5^2=100 ・・・めでたし、めでたし。
＃容器の傾けで、πがとれてしまうのが不思議で面白いです。
カルピスさんからのコメントです。（平成２９年８月１８日付け）
私は、πを消すには「曲面」の無い立体に変える必要があると考えました。底面（ｒ＝５）の
円に内接する正方形の面積は５０ｃｍ2。だから、高さ ２ｃｍの直方体を考えれば１００ｃｍ3
になる。
高さ４ｃｍ分の円柱の体積と（円－正方形）の面積ｘ高さ２ｃｍの体積。この二つを除去しよ
うとしました。
計算すると、１５０π－１００ を除去するには・・・。それも、１７πと２３πを使ってと、無駄
な労力を使った次第です。
