チラッと見て、解いてみようかなと思わせる問題をいくつか置いておきます。

（１）　等式　（１＋１/ａ）（１＋１/ｂ）＝２　を満たす自然数の組（ａ，ｂ）をすべて求めよ。

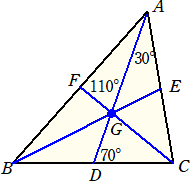
（２）　△ＡＢＣの辺ＢＣ、ＣＡ、ＡＢの中点をそれぞれＤ、Ｅ、Ｆとする。∠ＡＦＣ＝１１０°、
　　∠ＡＤＣ＝７０°で、∠ＣＡＤ＝２０°のとき、∠ＡＢＥの大きさを求めよ。

　　　　

（３）　ａ、ｂ は実数で、０＜ａ＜ｂ　、ａ＋ｂ＝２　のとき、０＜ａ＜１＜ｂ＜２　であることを示せ。

（４）　任意の自然数ｍに対して、（ｍ²）！ は、（ｍ！）^m+1 の倍数であることを示せ。

（例）　ｍ＝２　のとき、（ｍ²）！＝４！＝２４　は、（ｍ！）^m+1＝２³＝８ の倍数である。
　　　ｍ＝３　のとき、（ｍ²）！＝９！＝362880　は、（ｍ！）^m+1＝６⁴＝1296 の倍数である。
　　　実際に、362880÷1296＝280　で割り切れる。

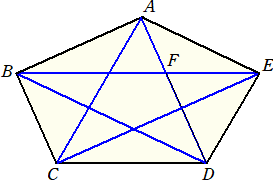
（５）　凸５角形があり、任意の対角線は、その対角線に交わらない辺に必ず平行とする。
　　このとき、その辺と対角線の比は常に一定になる。比の値を求めよ。

　　

（６）　２以上の自然数ｎの約数を小さい順に、 ｘ₁(=1)、ｘ₂、ｘ₃、・・・、ｘ_ｋ-1、ｘ_ｋ(=ｎ) とする。
　　このとき、　ｘ₁ｘ₂＋ｘ₂ｘ₃＋・・・＋ｄ_ｋ-1ｘ_ｋ＜ｎ²　であることを示せ。

（例）　ｎ＝６　のとき、約数は、１、２、３、６　なので、１・２＋２・３＋３・６＝２６＜６²


（解）（１）　等式より、（ａ＋１）（ｂ＋１）＝２ａｂ　なので、　（ａ−１）（ｂ−１）＝２

　　　　　よって、　（ａ−１，ｂ−１）＝（２，１）、（１，２）　より、（ａ，ｂ）＝（３，２）、（２，３）

（２）　中点連結定理より、ＡＣとＦＤは平行なので、∠ＦＤＧ＝３０°

　　∠ＡＤＢ＝１１０°なので、４点Ｂ、Ｄ、Ｇ、Ｆは同一円周上にある。

　　よって、　∠ＡＢＥ＝∠ＦＤＧ＝３０°

（３）　ａ＝２−ｂ＞０　より、ｂ＜２　である。ａｂ＝ｋ　とおくと、ａ、ｂは、２次方程式

　　　Ｆ（ｘ）＝ｘ²−２ｘ＋ｋ＝０　の２つの実数解である。

　よって、Ｆ（ｘ）＝（ｘ−１）²＋ｋ−１　より、軸の式は、ｘ＝１

　したがって、　０＜ａ＜１＜ｂ＜２　である。

（４）　ｍ²人をｍ人ずつｍ組に分ける方法の数は、

　　_ｍ²Ｃ_ｍ・_ｍ²-ｍＣ_ｍ・・・・・_2ｍＣ_ｍ÷ｍ！＝（ｍ²）！/（（ｍ！）^m+1）

　右辺は整数なので、（ｍ²）！ は、（ｍ！）^m+1 の倍数である。　　（終）

（５）　四角形ＥＦＤＧが平行四辺形となるように点Ｇをとる。

　

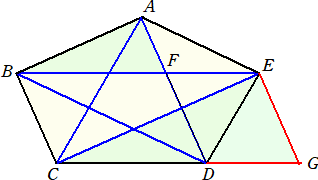
ＢＣ＝ｘ、ＣＤ＝ｙ とおく。ＢＤとＡＥは平行なので、ＢＤ ： ＡＥ＝１ ： ｒ （ｒ＞０）　とすると、

　ＡＦ＝ｒｘ　、ＥＦ＝ｒｙ　である。ＢＦ ： ＡＦ＝ＣＧ ： ＥＧ　より、　ｙ ： ｒｘ＝（ｒ＋１）ｙ ： ｘ なので、

　１ ： ｒ＋１＝ ｒ ： １　となるので、ｒ²＋ｒ−１＝０　これを解いて、ｒ＝（−１）/２

　このとき、　ＢＣ ： ＡＤ＝ｘ ： （ｒ＋１）ｘ＝２ ： ＋１

　ＣＤ ： ＢＥ＝ｙ ： （ｒ＋１）ｙ＝２ ： ＋１

　ＤＥ ： ＣＡ＝｛1/（１＋ｒ）｝ｘ ： ｛ｒ/（１＋ｒ）｝ｘ ＋ｒｘ＝１ ： ｒ²＋２ｒ

　ここで、ｒ²＝１−ｒ　なので、ＤＥ ： ＣＡ＝１ ： １＋ｒ＝２ ： ＋１

同様にして、　ＥＡ ： ＢＤ＝ＡＦ ： ＦＤ＝ｒｘ ： ｘ＝ｒ ： 1＝１ ： １/ｒ

　ここで、ｒ²＝１−ｒ　より、　１＋ｒ＝１/ｒ　なので、ＥＡ ： ＢＤ＝１ ： １＋ｒ＝２ ： ＋１

　ＡＢ ： ＣＥ＝ＢＦ ： CG＝ｙ ： （ｒ＋１）ｙ＝１ ： １＋ｒ＝２ ： ＋１

　以上から、辺と対角線の比は常に一定で、２ ： ＋１ となる。

（６）　題意より、　ｘ₁ｘ_ｋ＝ｎ、ｘ₂ｘ_ｋ-1＝ｎ、ｘ₃ｘ_ｋ-2＝ｎ、・・・　なので、

　ｘ₁ｘ₂＋ｘ₂ｘ₃＋・・・＋ｄ_ｋ-1ｘ_ｋ

＝（ｎ/ｘ_ｋ）（ｎ/ｘ_ｋ-1）＋（ｎ/ｘ_ｋ-1）（ｎ/ｘ_ｋ-2）＋・・・＋（ｎ/ｘ₂）（ｎ/ｘ₁）

　ここで、　ｘ₁≧１、ｘ₂≧２、ｘ₃≧３、・・・、ｘ_ｋ-1≧ｋ−１、ｘ_ｋ≧ｋ　であるので、

≦ｎ²（１/ｋ（ｋ−１）＋１/（ｋ−１）（ｋ−２）＋・・・＋１/（２・１））

＝ｎ²（１/（ｋ−１）−１/ｋ＋１/（ｋ−２）−１/（ｋ−１）＋・・・＋１−１/２）

＝ｎ²（１−１/ｋ）＜ｎ²