ｙ軸上の点Pを通る直線Lは、y=(1/4)ｘ² と２点A、Bで交わり、y=aｘ²　(a＞1/4) と２点C、D
で交わる。ただし、点Bの x 座標が 2 で、BD：DP：PC=1：3：4 とする。

　このとき、次の問いに答えよ。

(1)　a の値を求めよ。
(2)　直線 L の式を求めよ。
(3)　AP：CP を求めよ。

　混乱してしまい解けません。お願い致します。


（コメント）　面白そうだったので解いてみた。

　題意より、下図を得る。

　　

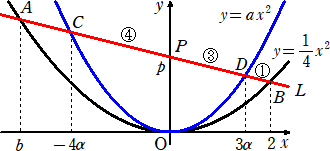
(1)　３α：２−３α＝３：１　より、　３α＝６−９α　なので、　α＝１/２

　　また、Ｂ（２，１）で、Ｃ（−２，４ａ）、Ｄ（３/２，９ａ/４）より、

　　４ａ−１：９ａ/４−１＝８：１　を解いて、　ａ＝１/２

(2)　Ｃ（−２，２）、Ｄ（３/２，９/８）より、直線 L の傾きは、（２−９/８）/（−２−３/２）＝−１/４

　なので、直線 L の式は、　ｙ＝（−１/４）（ｘ＋２）＋２＝（−１/４）ｘ＋３/２

(3)　（１/４）ｘ²＝（−１/４）ｘ＋３/２　より、　ｘ²＋ｘ−６＝０　なので、　ｘ＝−３、２

　　よって、　AP：CP＝３：２　となる。


＃標準的ないい問題でしたね！