原点をOとするxy平面上で、第１象限にある点(a，b)を通る傾きが負の直線とx軸、y軸との
交点をA、Bとする。このとき、△OABの周の長さの最小値はいくらか。


（コメント）　直感で、点(a，b)を通る直角２等辺三角形を考えて、(２＋)(ａ＋ｂ) ですか？


　らすかるさんからのコメントです。（平成２９年７月３０日付け）

　例えば、a=1000000、b=0.000001のとき直感的に「約2000000」（＝約2a）とわかりますので、
(２＋)(ａ＋ｂ) にはならないですね。


　ＨＮ「Ｄ」さんからのコメントです。（平成２９年７月２９日付け）

　我疑う故に存在する我 (デカルト) 曰く；　2 (a + b + Sqrt[2] Sqrt[a b])


　Ｓ（Ｈ）さんからのコメントです。（平成２９年７月３０日付け）

　2 (a + b + Sqrt[2] Sqrt[a b]) と宣ふ方が存在。真偽如何?


（コメント）　ａ＝２、ｂ＝１として、Grapesにグラフを描かせてみた。


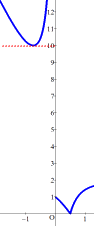
　　左のグラフにおいて、直線の傾きｍ＜０から最小値は１０と読み取れ、

　　　2 (a + b + Sqrt[2] Sqrt[a b]) ＝１０

　　　(2+√2)(a+b) ＝１０．２４２６・・・

　から、最小値は、2 (a + b + Sqrt[2] Sqrt[a b]) 　が正解のようですね！

　　直角２等辺三角形じゃないときに最小になるのか．．．。





　DD++さんからのコメントです。（平成２９年７月３１日付け）

　エレガントな解法をやっと見つけたので、やっと解答。

　直角三角形の周長は、斜辺で接する傍接円の直径に等しいことが少し考えるとわかりま
す。
　　　　

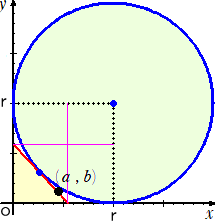
　第一象限にあり、x軸とy軸に接し、(a,b) を通る接線が存在する条件は、

　　(a-r)²+(b-r)²≧r²　つまり、　r≦a+b-√(2ab)　、a+b+√(2ab)≦r

　このうち 第一象限の三角形の傍接円になりうるのは、　a+b+√(2ab)≦r　のときのみ。

　よって、この三角形の周長の最小値は、2r = 2(a+b+√(2ab)) で、そうなるのは、x軸とy軸
に接し、(a,b) を通る円（大きい方）の (a,b) における接線が斜辺になるとき。


　らすかるさんからのコメントです。（平成２９年７月３１日付け）

　なるほど、エレガントですね。私はそのようなエレガントな解答が思い付きませんでしたの
で、

・斜辺とx軸の角度をθと置いて周の長さを三角関数で表すと、

　周の長さは、　bcosθ/sinθ+asinθ/cosθ+b/sinθ+a/cosθ+a+b

・t=tan(θ/2) とおいて、t の式にすると、周の長さは、　{(2a-b)t+b}/{t(1-t)}+b

・この式の増減を調べて最小値を得る

という力技でゴリゴリ計算しました。
（といっても比較的簡単な式になったので、計算は大したことありませんでした。）


（コメント）　本当にエレガントな解答ですね！感動しました。傍接円の性質にあらためて魅
　　　　　　入られました。DD++さんに感謝します。

　点（ａ，ｂ）を通る直線を、ｘ/ｈ＋ｙ/ｋ＝１　とおいて、　ａ/ｈ＋ｂ/ｋ＝１

　そのとき、三角形の周の長さＬは、　Ｌ＝ｈ＋ｋ＋√（ｈ²＋ｋ²）　となるので、ラグランジュの
乗数を用いて何とかしようとしましたが、煩雑な計算に挫折しました。らすかるさんのような手
順でやればよかったのかな？


　Ｓ（Ｈ）さんからのコメントです。（平成２９年７月３１日付け）

　点（a，b)を通る超平面を、x/α+y/β=1　とおいて、

　　a/α+b/β=1　と　α+ Sqrt[α² + β²] + β = k　が接するように k を定めればよい。

　第２式から、　２αβ−２ｋα−２ｋβ＋ｋ²＝０

　これに、第１式から得られる　β＝ｂα/（α−ａ）　を代入して整理すると、

　２（ｂ−ｋ）α²＋（２ｋａ−２ｋｂ＋ｋ²）α−ａｋ²＝０

　この判別式を求めると、　Ｄ＝ｋ²(4 a² + 4 b² - 4 a k - 4 b k + k²)

　　Ｄ＝０　から ｋ を求めると、　ｋ＝2 (a + b ± Sqrt[2] Sqrt[a b])

　これより、瞬時に　ｋ＝2 (a + b + Sqrt[2] Sqrt[a b])　を得る。.

　また、点（a，b)を通る直線は、1次函数　y = m (x - a) + b で与えられるので、三角形の周

の長さは、　f(m)=Sqrt[(a m-b)^2/m^2+(b-a m)^2]+(a m-b)/m-a m+b　と表示される。

　これより、f(m) の最小値を求める発想でも求められる。

　冒頭の問題を自然に拡張すると、次の問題が考えられる。

　 原点をOとするxyz空間で、第１象限にある点 (a，b，c) を通る超平面と x軸、y軸、z軸との
交点をA、B、Cとする。面積の和　△OAB+△OBC+△OAC+△ABC の最小値はいくらか。


（コメント）　なるほど、接する場合を考えればいいんですね。


　デヴォン青木さんからのコメントです。（平成２９年８月２３日付け）

　座標平面上において、点A (1, 2) を通る直線Lがx軸とy軸の正の部分と交わるとし、その
交点をB、Cとするとき、三角形OBCの周の長さが最小になるように直線Lを定めよ。


　スモークマンさんからのコメントです。（平成２９年８月２４日付け）

　(0,0)、(1,2)を焦点に持つ楕円で、(p,0)、(0,q) を通るとする…

　楕円上の点を(x,y)とすると…、　√(x^2+y^2)+√((x-1)^2+(y-2)^2)=k

　p+√((p-1)^2+2^2)=q+√(1^2+(q-2)^2)・・・(1)

　直線L：x/p+y/q=1　より、　1/p+2/q=1・・・(2)

(1)、(2)から…、p=5/2、q=10/3

so…　x/(5/2)+y/(10/3)=1　より、直線L：2x/5+3y/10=1　すなわち、4x+3y=10　でしょうか？

ちなみに...この時の周長=5/2+10/3+√((5/2)^2+(10/3)^2)=10


　Ｓ（Ｈ）さんからのコメントです。（平成２９年８月２４日付け）

　束縛条件　1/x + 2/y = 1　(0＜x、0＜y)　のもとで、　x + y + Sqrt[x^2 + y^2]の最小値を

(1)　ラグランジュの未定乗数法（method of Lagrange multiplier）で解いて下さい。
(2)　また、1変数函数の極値問題に帰着させて解いて下さい。