自然対数の底 ｅ は、２．７１８２８１８２８４・・・ と続く無理数（循環しない無限小数）である。
通常、この値は、
鮒ひと鉢、ふた鉢、・・・
と暗記されるが、余りに味気ない。
実は、連分数に書き直すと、次のような美しい振る舞いをすることを最近知った。
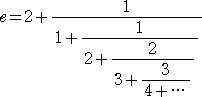
最も、正則連分数展開すると、
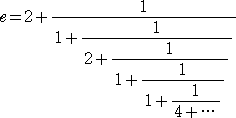
となって、美しさが失われるかに見える。
しかし、その先を求めると、
［２；１，２，１，１，４，１，１，６，１，１，８，１，１，１０，１，１，・・・］
となるらしい。（これは、連分数の表記法！）
（［２；１，２，１，１，４，１，１・・・］までは、手持ちの電卓で確認しましたが、その先の「６，１，１，・・・」に
ついては、現在未確認です。）
これを、じっと見つめると、何となく別な意味での美しい規則性が感じられるから不思議だ！
（追記） 平成１７年３月２６日 当ＨＰがいつもお世話になっている「らすかる」様より、連分
数展開の誤りのご指摘を頂いた。上記では、既に誤りは訂正済みである。
らすかる 様に感謝いたします。
我々が普通に知っている世界では不規則に並ぶ数字の列も、連分数展開すると鮮やか
に規則的に並ぶということが起きるようだ。
無理数
＝ １．４１４２１３５６２３７３１・・・・・ の正則連分数展開は［１；２，２，２，２，２，２，２，２，２，２，２，２，２，２，２，２，・・・］
無理数
＝ １．７３２０５０８０７５６８８８・・・・・ の正則連分数展開は［１；１，２，１，２，１，２，１，２，１，２，１，２，１，２，１，２，・・・］
このように、あるところから同じ数字が周期的に繰り返し表れる連分数は、循環連分数と
いわれ、
＝ 
＝ 
と表記される。（循環節の始めと終わりにドット（・）を打つのは、普通の数の場合と同様である。）
、 のような無理数は、２次の無理数（整数係数の２次方程式の無理数解）といわれる。
このとき、次の定理が知られている。
２次の無理数は循環連分数となり、逆に、循環連分数は２次の無理数である。
（Ｌａｇｒａｎｇｅ）
この定理より、自然対数の底 ｅ は、２次の無理数ではないので、循環連分数にはなりえ
ない。
また、よく知られた無理数として、
円周率 π ＝ ３．１４１５９２６５３５８９７９・・・・・
があるが、この正則連分数展開
π ＝ ［３；７，１５，１，２９２，１，１，１，２，１，３，・・・］
は、お世辞にも美しいとはいえない。
円周率については、次のような連分数展開が、とても美しい！
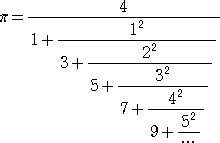
（追々記） 黄金比 φ は図形的な美を醸し出すが、実は数そのものでも美しいようだ。
黄金比 φ は、整数係数の２次方程式 φ2−φ−１＝０ の解であるので、Ｌａｇｒａｎｇｅ の
定理から、循環連分数となる。
φ2−φ−１＝０ より、 φ2＝φ＋１ なので、
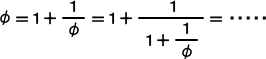
このことから、 φ＝
となる。 何と、単純で美しいのだろう！（追記） 黄金比について、当ＨＰ読者のＫ．Ｓ．さんよりメールを頂いた。
（平成２５年３月５日付け）
φ2−φ−１＝０ より、 φ2＝φ＋１ なので、
φ＝１＋１/φ
という見方をすれば、連分数表示が得られる。また、
φ＝√（１＋φ）
という見方をすれば、根号表示が得られる。
（追記） 平成２５年５月２３日付け
最近の大学入試で連分数を取り上げる大学が増えてきた。２０１１年の東京大学、２０１２
年の京都大学など。２０１３年度も順天堂大学医学部で出題された。来年度もこの流行が続
くのだろうか？
順天堂大学医学部（２０１３）
このとき、ａ、ｂ、ｃ、ｘ、ｙ の値を求めよ。
（解） 題意より、 ｙ＝１/（２＋ｙ） と書けるので、求める２次方程式は、 ｙ2＋２ｙ−１＝０
よって、 ａ＝１、ｂ＝２、ｃ＝−１ となる。
このとき、ｙ＞０ に注意して、 ｙ＝−１＋
また、 ｘ＝２/（１＋ｙ） なので、 ｘ＝
（終）京都大学 前期理系（２０１２）
さいころをｎ回投げて出た目を順に Ｘ1、Ｘ2、・・・、Ｘｎ とする。さらに
Ｙ1＝Ｘ1 、Ｙｋ＝Ｘｋ＋１/Ｙｋ-1 （ｋ＝２、・・・、ｎ）
によって、Ｙ1、Ｙ2、・・・、Ｙｎ を定める。 （１＋
）/２≦Ｙｎ≦１＋ となる確率 ｐｎ を求めよ。
（実験） さいころを１回投げて出た目の数を Ｘ1 とする。
このとき、Ｙ1＝Ｘ1 なので、 （１＋
）/２≦Ｙ1＝Ｘ1≦１＋ となる確率 ｐ1 を求めるには、 １．３６６・・・≦Ｘ1≦２．７３２・・・ すなわち、 Ｘ1＝２ のみより、 ｐ1 ＝１/６
さいころを２回投げて出た目の数を Ｘ1 、Ｘ2 とする。
このとき、Ｙ2＝Ｘ2＋１/Ｙ1＝Ｘ2＋１/Ｘ1 なので、 （１＋
）/２≦Ｙ2≦１＋ となる確率ｐ2 を求めるには、 １．３６６・・・≦Ｘ2＋１/Ｘ1≦２．７３２・・・
このとき、 （Ｘ1 ，Ｘ2）＝（１，１）、（２，１）、（２，２）、（３，２）、（４，２）、（５，１）、（６，１）
なので、求める確率 p2 は、 ｐ2 ＝７/３６
さいころを３回投げて出た目の数を Ｘ1 、Ｘ2 、Ｘ3 とする。
このとき、Ｙ3＝Ｘ3＋１/Ｙ2 、Ｙ2＝Ｘ2＋１/Ｘ1 なので、 （１＋
）/２≦Ｙ2≦１＋ となる確率 ｐ3 を求めるには、 １．３６６・・・≦Ｘ3＋Ｘ1/（Ｘ1Ｘ2＋１）≦２．７３２・・・
このとき、
（Ｘ1 ，Ｘ2 ，Ｘ3）＝（１，１，１）、（１，１，２）、（１，２，２）、（１，３，２）、（１，４，２）、（１，５，２）、
（１，６，２）、（２，１，１）、（２，１，２）、（２，２，１）、（２，２，２）、（２，３，１）、
（２，４，１）、（２，５，１）、（２，６，１）、（３，１，１）、（３，２，１）、（３，２，２）、
（３，３，２）、（３，４，２）、（３，５，２）、（３，６，２）、（４，１，１）、（４，２，１）、
（４，２，２）、（４，３，１）、（４，４，２）、（４，５，２）、（４，６，２）、（５，１，１）、
（５，２，１）、（５，２，２）、（５，３，２）、（５，４，２）、（５，５，２）、（５，６，２）、
（６，１，１）、（６，２，１）、（６，２，２）、（６，３，２）、（６，４，２）、（６，５，２）、
（６，６，２）
なので求める確率 p3 は、ｐ3 ＝４３/２１６
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
数列 １/６，７/３６，４３/２１６，・・・ は、
（１−（１/６））/５，（１−（１/６）2）/５，（１−（１/６）3）/５，・・・
と考えられるので、求める確率 pｎ は、ｐｎ ＝（１−（１/６）ｎ）/５ と予想される。 （終）
（コメント） 厳密には数学的帰納法で証明するところだが、数列の一般項を予想しただけで
も何点かはもらえるかな？
上記の実験では、そんなに部分点がもらえそうにないので、実験をヒントに解答をでっち上
げてみた。
（解） （１＋
）/２≦Ｙｎ≦１＋ となる確率が ｐｎ なので、同様に、Ｙｎ＜（１＋
）/２ となる確率を ｑｎ、１＋＜Ｙｎ となる確率を ｒｎ とおく。このとき、明らかに、 ｐｎ＋ｑｎ＋ｒｎ＝１ である。ここで、Ｙｎ≧１ である。
実際に、ｎ＝１のとき、 Ｙ1＝Ｘ1≧１ で、ｎ＝１のとき成り立つ。
Ｙｎ≧１と仮定すると、Ｙｎ+1＝Ｘｎ+1＋１/Ｙｎ≧１ で、Ｙｎ+1≧１
以上から、数学的帰納法により、 Ｙｎ≧１ が成り立つ。
ｐｎ+1 と ｐｎ の関係を調べるために、１．３６６・・・≦Ｘｎ+1＋１/Ｙｎ≦２．７３２・・・ において、
Ｙｎ≧１より、 Ｘｎ+1＝１ または ２ でなければならない。
Ｘｎ+1＝１ のとき、 ０．３６６・・・≦１/Ｙｎ≦１．７３２・・・ すなわち、（
−１）/２≦１/Ｙｎから、 Ｙｎ≦
＋１＝２．７３２・・・よって、１/６の確率で、この場合の確率は、ｐｎ＋ｑｎ となる。
Ｘｎ+1＝２ のとき、 ０≦１/Ｙｎ≦０．７３２・・・ すなわち、１/Ｙｎ≦
−１ から、Ｙｎ≧（
＋１）/２よって、１/６の確率で、この場合の確率は、ｐｎ＋ｒｎ となる。
以上から、 ｐｎ+1＝（１/６）（ｐｎ＋ｑｎ）＋（１/６）（ｐｎ＋ｒｎ）＝（１/６）（ｐｎ＋１）
ここで、 ｐ1 ＝１/６ である。
よって、 ｐｎ+1−１/５＝（１/６）（ｐｎ−１/５） から、
ｐｎ−１/５＝（１/６）ｎ-1（ｐ1−１/５）＝−（１/５）（１/６）ｎ
すなわち、求める確率は、 ｐｎ＝｛１−（１/６）ｎ｝/５ となる。 （終）
（コメント） 最初、（１＋
）/２ と １＋ にすごく違和感を感じたのですが、上記のように解いてみると、互いに巧妙な関係になっていて、練りに練られた問題になっている
ことに感動させられます。さすが京大ですね！
