いきます。そのとき、
・円は紙からはみ出さない
・円と円は重ならない(◎も×)
というルールを守った場合、円周の総和が+∞になる(鉛筆がいくらあっても足りない)ことは
ありますか？
らすかるさんからのコメントです。（平成２９年５月１０日付け）
あります。まず半径1の円を描きます。その隣に半径1/2の円を2個、並べて描きます。そ
の隣に半径1/4の円を4個、1列に並べて描きます。その隣に半径1/8の円を8個、1列に並
べて描きます。・・・
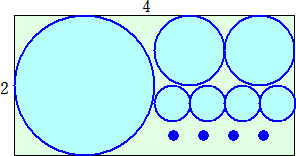
これをいくら続けても大きさ2×4の紙をはみ出ることはありませんが、円周は、
半径1の円→2π
半径1/2の円2個→π×2=2π
半径1/4の円4個→π/2×4=2π
半径1/8の円8個→π/4×8=2π
・・・・・・
のようになり総和は無限です。
もし、「円と円が接してはいけない」という条件がある場合は、それぞれの円の半径を、例
えば、0．9倍にして描けば各列の円周の合計が1.8πになり、やはり総和は無限になります。
源太さんからのコメントです。（平成２９年５月１０日付け）
正方形の中に円を3つ配置するとき、円周の長さの和を最大にするには？
らすかるさんからのコメントです。（平成２９年５月１０日付け）
正方形の1辺を1として、対角に半径(2-
)/2の円二つと残りの隙間に半径2-
/2-√(4-2)の円で円周の合計{8-3-2√(4-2)}π≒5.0032 が最大でしょうか。# 当然、円が重なったり含まれたりしてはダメですよね？
