紹介したいと思います。多分、この手の問題に不慣れな受検生を大いに悩ますのに十分な
難問でしたが、数学愛好家の視点では感動的な良問でした。
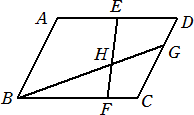
下の図において、四角形ABCDは平行四辺形であり、点Eは辺ADの中点である。
また、点Fは辺BC上の点で、BF:FC=3:1であり、点Gは辺CD上の点で、
CG:GD=2:1である。線分BGと線分EFとの交点をHとするとき、線分BHと線分HG
の長さの比を最も簡単な整数の比で表しなさい。
(解) 条件より、 AE=ED=2 とすると、△GBC∽△GID で、DI=2 となる点IがADの
延長上に取れる。このとき、△HBF∽△HIE より、BH:HI=3:4 で、GH=x とおくと、
x+3k : 4k−x = 2 : 1 (kは比例定数)
よって、 x+3k = 8k−2x から、 x=5k/3 となるので、
BH : HG = 3k : 5k/3 = 9 : 5 (終)
上記では、方程式を立てましたが、次のように解くことも可能でしょう。
(別解) 連比の考えを用いて、 BH:HI=3:4=9:12 、BG:GI=2:1=14:7 より、
BH=9、HI=12、BG=14、GI=7 と考えると、GH=5 となる。
よって、 BH : HG = 9 : 5 である。 (終)
S(H)さんからのコメントです、(平成29年3月10日付け)
座標を適当に設け、B=(0,0)、H=(18/7,9/14)、G=(4,1) より、 比=9:5
また、次の問題の(ウ)も学力上位者を意識しての、よく考えられた問題と言えます。
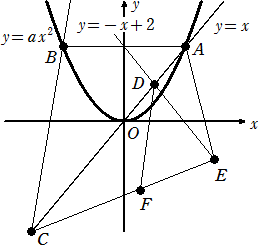
下の図において、点Oは原点で、点A、B、C、D、E、Fを図のように定める。
ただし、点Aのx座標は2で、線分ABはx軸に平行、点Cのx座標は負で、
AO:OC=2:3とする。さらに、点Eのx座標は3である。このとき、次の問いに答えな
さい。
(ア) aの値を求めよ。
(イ) 直線BCの式を求めよ。
(ウ) 線分DFが三角形ACEの面積を2等分するとき、点Fのx座標を求めよ。
(解) 問題の条件より、 A(2,2)、B(−2,2)、C(−3,−3)、E(3,−1) である。
(ア) y=ax2 が点Aを通るので、 2=4a より、 a=1/2
(イ) 傾きが5の直線で点Bを通るので、 y=5(x+2)+2=5x+12
(ウ) y=−x+2 と y=x を連立して、点D(1,1)である。∠ADE=90°で、AD=
DE=2
また、△ACE=4×3÷2+4×2÷2=10 なので、題意より、
△DCF : △DFE = CF : FE = 5 : 3
となるように点Fを定めればよい。点Fのx座標をxとすると、 x+3 : 3−x = 5 : 3
よって、 3x+9=15−5x より、 8x=6 なので、 x=3/4 (終)
(コメント) 座標幾何の問題として一つ一つ地道に求めていくことも出来るが、上記のように
相似比を用いて解決するのが最も簡潔な解でしょう。
次の確率の問題は、手数が掛かりすぎて試験時間内では厳しいような...。
片方の面が白、もう片方の面が黒である同じ大きさで平らな円形の石が6個ある。これら6個の石の
白と黒の両面には、1、2、3、4、5、6の数がそれぞれ1つずつ書かれており、両面に書かれた数は
同じである。
大、小2つのさいころを同時に1回投げ、出た目の数によって、次の操作1、操作2を順に行うことと
する。
操作1: 大きいさいころの出た目の数の約数と同じ数が書かれた石をすべて裏返す。
操作2: 小さいさいころの出た目の数の約数と同じ数が書かれた石をすべて裏返す。
ただし、大、小2つのさいころはともに、1から6までのどの目が出ることも同様に確からしいものとす
る。
今、すべての石の上の面が白であるとき、次の問いに答えなさい。
(ア) すべての石の白の面が上となる確率を求めよ。
(イ) 白の面が上になっているすべての石の、白の面に書かれた数の積が60の倍数となる確率を求
めよ。
(解) 起こり得るすべての場合の数は、36通り
(ア) ゾロ目の出る確率なので、 6/36=1/6
(イ) 表を作ると、
