・不思議な関係　　　　　　　　　　　　　　　　　Ｓ．Ｈ氏

　次の等式
　　　　　　　　　２７⁵＋８４⁵＋１１０⁵＋１３３⁵＝１４４⁵

は、１９６６年に発見されたものである。実際に確かめてみると、

となり、成り立っている。（計算には、ＥｘｃｅｌのＶＢＡを利用）

　このような等式は、どのようなきっかけで発見されたのだろうか？


（追記）　ｘ^ｋ＋ｙ^ｋ＋・・・＋ｚ^ｋ＝Ｎ^ｋ　のような形の不定方程式は、フェルマーの問題の延長
　　　　で昔から考えられてきたようである。（もちろん、文字は全て自然数とする。）

　中でも有名なものは、　　ｘ³＋ｙ³＋ｚ³＝Ｎ³　　という形の方程式らしい。

　　この解は、無数にあることが知られている。

　直ぐ思いつくものとしては、　（ ｘ ， ｙ ， ｚ ）＝（ ３ ， ４ ， ５ ） の場合で、このとき、Ｎ＝６
である。（→　参考：ピタゴラスより美しい？）

　あまり自明でないものとしては、例えば　（ ｘ ， ｙ ， ｚ ）＝（ ２５ ， ３１ ， ８６ ） の場合だ
ろう。この場合、Ｎ＝８８　である。

　何れも一つ解が見つかれば、その比例定数倍したものも解になるので、解は無数にある
というわけである。

　この形の方程式の一般解が、オイラーにより与えられている。

　講談社ブルーバックス　現代数学小事典（寺阪英孝　編）に、その記載（ｐ．１６７）がある。
ただ、その記載の通りに計算すると誤った答が導かれるので、多分誤植があるのだろう。

　いくつか実験をして、次の式が正しいものと判断される。

　　　　ｘ＝－（ａ²＋３ｂ²）²＋（ｃ²＋３ｄ²）（ａｃ＋３ｂｄ＋３ａｄ－３ｂｃ）

　　　　ｙ＝　（ａ²＋３ｂ²）²－（ｃ²＋３ｄ²）（ａｃ＋３ｂｄ－３ａｄ＋３ｂｃ）

　　　　ｚ＝　（ｃ²＋３ｄ²）²－（ａ²＋３ｂ²）（ａｃ＋３ｂｄ＋３ａｄ－３ｂｃ）

　　　　Ｎ＝　（ｃ²＋３ｄ²）²－（ａ²＋３ｂ²）（ａｃ＋３ｂｄ－３ａｄ＋３ｂｃ）

　表計算ソフト Ｅｘｃｅｌ のセルに数式を設定して、いろいろ遊んでみたのが下図である。

　　　　　

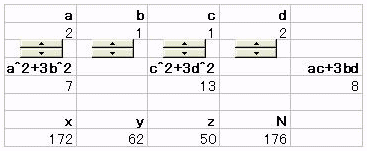
　さて、上記のオイラーが与えたと言われる数式であるが、

　　　　ｘ³＋ｙ³＋ｚ³＝Ｎ³

が本当に成り立つのか、確認しようとする気が失せるほど長い。オイラーは、どのようなア
イデアのもとに、この数式を発見したのだろうか？むしろ、そちらの方に関心がある。

（追記）　平成１８年５月１４日　広島工業大学の大川研究室より、この話題について、いろ
　　　　　いろお教えいただいた。

　良く本に載っているオイラーの式と言われる物が間違っている場合があるということであ
るが、確かに私がインターネットで検索したＨＰの中にも、式の通り計算しても結果が得ら
れない場合があった。（実際に、確認済み）式の複雑さからか、なかなか検証困難なため
だろうか？

　また、ＨＰサイト「コンピュータ数論」をご紹介いただいた。上記の話題についてよくまとめ
られていて大いに参考になった。そこでは、

　ｘ ，ｙ ，ｚ ，Ｎ を整数とするとき、

　　　ｘ³＋ｙ³＋ｚ³＝Ｎ³ の既約パラメータ解は無数に存在する

ことが示されている。とても感動的な結果である。

　また、ｘ³＋ｙ³＋ｚ³＝Ｎ³ の解として、ラマヌジャンは次の式を残しているようだ。

　　ｘ＝３ａ²＋５ａｂ－５ｂ²

　　ｙ＝４ａ²－４ａｂ＋６ｂ²

　　ｚ＝５ａ²－５ａｂ－３ｂ²

　　Ｎ＝６ａ²－４ａｂ＋４ｂ²

　オイラーの式と比べて、その簡素さにただ驚くばかりである。

　また、オイラーの時代には、　ｘ⁴＋ｙ⁴＋ｚ⁴＝Ｎ⁴ には解はないだろうと予想されていたら
しいが、反例（Ｅｌｋｉｅｓ　１９８７年）が発見されたという。Ｆｒｙｅ による最小解は、

　　　９５８００⁴＋２１７５１９⁴＋４１４５６０⁴＝４２２４８１⁴

であるそうだ。

（追記）　平成１８年５月１７日　広島工業大学の大川研究室からの連絡で、上記のオイラー
　　　　　の式が正しいことが確認された。数式処理ソフトMathematicaを用いられたそうだ。

　手計算で確認しようと思えば、次のように考えるのが筋だろう。

　Ａ＝ａ²＋３ｂ²　、Ｂ＝ａｃ＋３ｂｄ　、Ｃ＝ｃ²＋３ｄ²　、Ｄ＝３ａｄ－３ｂｃ　とおくと、

　　　　ｘ＝－Ａ²＋Ｃ（Ｂ＋Ｄ）　、　ｙ＝　Ａ²－Ｃ（Ｂ－Ｄ）

　　　　ｚ＝　Ｃ²－Ａ（Ｂ＋Ｄ）　、　Ｎ＝　Ｃ²－Ａ（Ｂ－Ｄ）

　このとき、　ｘ＋ｙ ＝ ２ＣＤ 、　ｘｙ ＝ Ｃ²Ｄ²－（Ａ²－ＢＣ）²　なので、

　ｘ³＋ｙ³ ＝ （ｘ＋ｙ）³－３ｘｙ（ｘ＋ｙ）

　　　　　　＝ ８Ｃ³Ｄ³－６ＣＤ（Ｃ²Ｄ²－（Ａ²－ＢＣ）²）

　　　　　　＝ ２Ｃ³Ｄ³＋６ＣＤ（Ａ²－ＢＣ）²

同様にして、　Ｎ－ｚ ＝ ２ＡＤ　、　Ｎｚ ＝ （Ｃ²－ＡＢ）²－Ａ²Ｄ²　なので、

　Ｎ³－ｚ³ ＝ （Ｎ－ｚ）³＋３Ｎｚ（Ｎ－ｚ）

　　　　　　 ＝ ８Ａ³Ｄ³＋６ＡＤ（（Ｃ²－ＡＢ）²－Ａ²Ｄ²）

　　　　　　 ＝ ２Ａ³Ｄ³＋６ＡＤ（Ｃ²－ＡＢ）²

　これらが等しいことを言えばいいのだが、．．．。

つまり、　２Ｃ³Ｄ³＋６ＣＤ（Ａ²－ＢＣ）²＝２Ａ³Ｄ³＋６ＡＤ（Ｃ²－ＡＢ）²　から

　　（Ａ³－Ｃ³）Ｄ³＝３Ｄ（Ｃ（Ａ²－ＢＣ）²－Ａ（Ｃ²－ＡＢ）²）

　　　　　　　　　　 ＝３Ｄ（ＣＡ⁴－２Ａ²ＢＣ²＋Ｂ²Ｃ³－ＡＣ⁴＋２Ａ²ＢＣ²－Ａ³Ｂ²）

　　　　　　　　　　 ＝３Ｄ（ＣＡ⁴＋Ｂ²Ｃ³－ＡＣ⁴－Ａ³Ｂ²）

　　　　　　　　　　 ＝３Ｄ（ＡＣ（Ａ³－Ｃ³）－Ｂ²（Ａ³－Ｃ³））

　　　　　　　　　　 ＝（Ａ³－Ｃ³）（３ＡＣ－３Ｂ²）Ｄ

が成り立つことを示せばいいのだが、．．．。

　ここで、

　３ＡＣ－３Ｂ²＝３（ａ²＋３ｂ²）（ｃ²＋３ｄ²）－３（ａｃ＋３ｂｄ）²

　　　　　　　　＝３ａ²ｃ²＋９ａ²ｄ²＋９ｂ²ｃ²＋２７ｂ²ｄ²－３ａ²ｃ²－１８ａｂｃｄ－２７ｂ²ｄ²

　　　　　　　　＝（３ａｄ－３ｂｃ）²＝Ｄ²

なので、　（Ａ³－Ｃ³）Ｄ³＝（Ａ³－Ｃ³）（３ＡＣ－３Ｂ²）Ｄ　が成り立つ。

　よって、ｘ³＋ｙ³ ＝ Ｎ³－ｚ³　より、　ｘ³＋ｙ³＋ｚ³＝Ｎ³　であることが言える。


（コメント）　厳密な証明とは言えないが、何とか強引に、成り立つことの確かさを確認する
　　　　　　ことができて「ホッ！」としている。


（追記）　平成１８年５月１８日、当ＨＰがいつもお世話になっている、らすかるさんから、ラマ
　　　　ヌジャンの式について、その証明をいただいた。

　風邪を引いて体調が絶不調で、かつ超多忙（従って、休めない．．．(T.T) ）ということで、
整理が覚束なく、この日のアップになってしまいました。らすかるさん、申し訳ないです。

　　ｘ＝３ａ²＋５ａｂ－５ｂ²　、　ｙ＝４ａ²－４ａｂ＋６ｂ²　

　　ｚ＝５ａ²－５ａｂ－３ｂ²　、　Ｎ＝６ａ²－４ａｂ＋４ｂ²

について、ｘ³＋ｙ³＋ｚ³＝Ｎ³　が成り立つことを示す。

　高々３乗の計算なので腕力があれば何でもないが、らすかるさんは次のように工夫された。

（証明）　ｕ＝（ａ＋ｂ）/２、 ｖ＝（ａ－ｂ）/２ とおいて、それぞれの変数に代入して整理すると、

　　　　ｘ＝３ｕ²＋１６ｕｖ－７ｖ²　、　ｙ＝６ｕ²－４ｕｖ＋１４ｖ²　

　　　　ｚ＝－３ｕ²＋１６ｕｖ＋７ｖ²　、　Ｎ＝６ｕ²＋４ｕｖ＋１４ｖ²

これより、
　　　　　　　ｘ＋ｚ＝３２ｕｖ　、　ｘｚ＝（１６ｕｖ）²－（３ｕ²－７ｖ²）²

　　　　　　　Ｎ－ｙ＝８ｕｖ　、　Ｎｙ＝（６ｕ²＋１４ｖ²）²－（４ｕｖ）²

なので、

　ｘｚ（ｘ＋ｚ）＋Ｎｙ（Ｎ－ｙ）

＝３２ｕｖ｛（１６ｕｖ）²－（３ｕ²－７ｖ²）²｝＋８ｕｖ｛（６ｕ²＋１４ｖ²）²－（４ｕｖ）²｝

＝３２ｕｖ｛（１６ｕｖ）²－（３ｕ²－７ｖ²）²｝＋３２ｕｖ｛（３ｕ²＋７ｖ²）²－（２ｕｖ）²｝

＝３２ｕｖ｛（１６ｕｖ）²－（２ｕｖ）²｝＋３２ｕｖ｛（３ｕ²＋７ｖ²）²－（３ｕ²－７ｖ²）²｝

＝３２ｕｖ・２５２（ｕｖ）²＋３２ｕｖ・８４（ｕｖ）²

＝１０７５２（ｕｖ）³

＝２⁹・２１（ｕｖ）³

ところで、

　（ｘ＋ｚ）³－（Ｎ－ｙ）³＝（３２ｕｖ）³－（８ｕｖ）³＝２¹⁵（ｕｖ）³－２⁹（ｕｖ）³＝２⁹・６３（ｕｖ）³

よって、

　　　（ｘ＋ｚ）³－（Ｎ－ｙ）³＝ｘ³＋ｙ³＋ｚ³－Ｎ³＋３｛ｘｚ（ｘ＋ｚ）＋Ｎｙ（Ｎ－ｙ）｝

より、

　　　ｘ³＋ｙ³＋ｚ³－Ｎ³＝２⁹・６３（ｕｖ）³－３・２⁹・２１（ｕｖ）³＝０

したがって、　　ｘ³＋ｙ³＋ｚ³＝Ｎ³　が成り立つ。（証終）


（コメント）　とても洗練された証明で、分かりやすいですね！高校１年レベルの実力テスト
　　　　　　問題に使えそうな雰囲気です。


　ＧＡＩ さんから、上記に関連した話題の提供です。（平成２６年１月１９日付け）

　どうやって探し出すんだろう？


　攻略法さんからのコメントです。（平成２６年１月１９日付け）

　A+B-C=0　のとき、(X-A)²+(X-B)²+(X+C)²=(X+A)²+(X+B)²+(X-C)²　が成り立つので、

　1+2-3=0 より、　(X-1)²+(X-2)²+(X+3)²=(X+1)²+(X+2)²+(X-3)² において、x=6　とおくと、

　　　5²+4²+9²=7²+8²+3²

　同様に、2+21-23=0　より、　(X-2)²+(X-21)²+(X+23)²=(X+2)²+(X+21)²+(X-23)² において、

x=66　とおくと、　64²+45²+89²=68²+87²+43²

　2+77-79=0　より、　(X-2)²+(X-77)²+(X+79)²=(X+2)²+(X+77)²+(X-79)² において、

x=866　とおくと、　864²+789²+945²=868²+943²+787²

　2+921-923=0　より、　(X-2)²+(X-921)²+(X+923)²=(X+2)²+(X+921)²+(X-923)² において、

x=2866　とおくと、　2864²+1945²+3789²=2868²+3787²+1943²

　2+19077-19079=0　より、

　　(X-2)²+(X-19077)²+(X+19079)²=(X+2)²+(X+19077)²+(X-19079)² において、

x=42866　とおくと、　42864²+23789²+61945²=42868²+61943²+23787²


類題　次の式を計算してみてください。

　(a) 642864² + 123789² + 561945² - (242868² + 761943² + 323787²)
　(b) 42864² + 23789² + 61945² - (42868² + 61943² + 23787²)
　(c) 2864² + 3789² + 1945² - (2868² + 1943² + 3787²)
　(d) 864² + 789² + 945² - (868² + 943² + 787²)
　(e) 64² + 89² + 45² - (68² + 43² + 87²)
　(f) 4² + 9² + 5² - (8² + 3² + 7²)

　(g) 642864² + 123789² + 561945² - (242868² + 761943² + 323787²)
　(h) 64286² + 12378² + 56194² - (24286² + 76194² + 32378²)
　(i) 6428² + 1237² + 5619² - (2428² + 7619² + 3237²)
　(j) 642² + 123² + 561² - (242² + 761² + 323²)
　(k) 64² + 12² + 56² - (24² + 76² + 32²)
　(l) 6² + 1² + 5² - (2² + 7² + 3²)

　(m) 642864² + 123789² + 561945² - (242868² + 761943² + 323787²)
　(n) 4286² + 2378² + 6194² - (4286² + 6194² + 2378²)
　(o) 28² + 37² + 19² - (28² + 19² + 37²)

　（答え）はすべて０。


（コメント）　不思議な関係ですね！


　当ＨＰ読者のＨＮ「Ｋ．Ｆ．」さんより、メールでご投稿いただきました。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（令和４年４月２２日付け）

　私は、上記の後半に載っている式を、岩波書店の『偏愛的数学 驚異の数』の中で見つけ
ました。

　　123789^2 + 561945^2 + 642864^2 ＝ 242868^2 + 761943^2 + 323787^2

　自分でもなんとか作れないものかと試みた結果、いくつかできたのですが、うまく説明でき
ません。「不思議な関係」の式の作り方を、わかりやすく解説した文献やサイトを探していま
す。よろしくお願いします。


（コメント）　Ｋ．Ｆ．さん、ご投稿ありがとうございます。メールにWordファイルが添付されてい
　　　　　　ましたが、セキュリティの関係で開けることが出来ませんでした。悪しからずご了承
　　　　　　ください。


　Ｋ．Ｆ．さんからのコメントです。（令和４年５月１２日付け）

　ワードが開けなかったとのことですので、中身を再送信しました。

　123789^2 + 561945^2 + 642864^2 ＝ 242868^2 + 761943^2 + 323787^2

について、まず、数値を縦に並べ、上 (左辺)と下 (右辺)を見比べると、2つのことがわかり
ます。

1 2 3 7 8 9 　① 万・千・百・十の位の数字は上下同じで、３つの数字の差が一定

5 6 1 9 4 5　　　万の位： 2・6・4　と　4・6・2、　千の位： 3・1・2　と　2・1・3

6 4 2 8 6 4　 　 百の位： 7・9・8　と　8・9・7、　十の位： 8・4・6　と　6・4・8

2 4 2 8 6 8 ② 十万・一の位の数字は、３つの和が上下等しく、２乗の和も等しい

7 6 1 9 4 3 　　十万の位： 1 + 5 + 6 ＝ 2+ 7 + 3　、 1² + 5² + 6² = 2² + 7² + 3²

3 2 3 7 8 7 　　一の位： 9 + 5 + 4 ＝ 8+ 3 + 7　、　9² + 5² + 4² = 8² + 3² + 7²

　そこで、①、②のような数字の例を探し出しました。

③　３つの数字の差が一定の例

　　1・2・3、　 1・3・5、　 1・4・7、 　1・5・9　　2・3・4、 　2・4・6、　 2・5・8、 　3・4・5

　　3・5・7、 　3・6・9、 　4・5・6、 　4・6・8　　5・6・7、　 5・7・9、　 6・7・8、 　7・8・9

④　３つの数字の和が等しく、２乗和も等しい例

　　3²+3²+0²＝1²+1²+4²、 2²+2²+5²＝1²+4²+4²、 0²+4²+5²＝6²+2²+1²、 5²+5²+2²＝3²+3²+6²

　　1²+5²+6²＝7²+3²+2²、 0²+6²+6²＝8²+2²+2²、 0²+5²+7²＝8²+3²+1²、 6²+6²+3²＝4²+4²+7²

　　0²+5²+8²＝9²+2²+2²、 7²+6²+2²＝3²+4²+8²、 0²+7²+7²＝9²+4²+1²、 7²+7²+1²＝3²+3²+9²

　　1²+6²+8²＝2²+4²+9²、 8²+5²+5²＝7²+7²+4²、 3²+7²+8²＝4²+5²+9²、 8²+8²+5²＝6²+6²+9²

③と④の例を組み合わせて、新しい式を作りました。

　　　　　　　　　　　　 上 (左辺)　 下 (右辺)

1 2 3 7 8 9 　　十万の位： 1・6・8　と　2・4・9

6 2 7 8 5 4 　　万の位： 2・2・5　と　1・4・4

8 5 8 9 5 2 　　千の位： 3・7・8　と　4・5・9

2 1 4 7 7 8 　　百の位： 7・8・9　と　7・8・9

4 4 5 8 7 6 　　十の位： 8・5・5　と　7・7・4

9 4 9 9 4 1　　 一の位： 9・4・2　と　8・6・1

　これより、

　 　123789²+ 627854²+ 858952²= 214778²+ 445876²+ 949941²

　数値を逆にしても式が成立します。

　　 987321²+458726²+ 259858²＝ 877412²+ 678544²+ 149949²　　

　桁数がもっと多くても式が作れます。

　　123456789²+ 572347235²+ 637892674²= 756783453²+361238347²+ 215674898²

　　987654321²+ 532743275²+ 476298736²= 354387657²+743832163²+ 898476512²


＃ネット検索すると、様々な国の言葉で「不思議な関係」の式を紹介していますが、
　987321²+532275²+・・・のように、数値を逆にしても式が成立することに言及したサイトは見
　つけられませんでした。


（コメント）　Ｋ．Ｆ．さんの数式の作り方から「本当に出来るのかな？」という思いがあったの
　　　　　　ですが、成立しているということは正に「不思議な関係」ですね。再度Ｗｏｒｄの内容
　　　　　　を送信していただいたＫ．Ｆ．さんに感謝します。



　　以下、工事中