一辺の長さが t の正三角形ABCがある。今、△ABCの重心を原点Oに、頂点Aをｙ軸上の
正の部分に置く。このとき、直線 ｙ＝ｘ に関して各頂点の対称点をそれぞれA’、B’、C’、ま
た、直線 ｙ＝−ｘ に関して、各頂点の対称点をそれぞれA”、B”、C”とする。

(１)　３つの三角形△ABC、△A’B’C’、△A”B”C”が重なる部分の面積S₁

(２)　３つの三角形△ABC、△A’B’C’、△A”B”C”が重なって囲まれる部分の面積S₂

は何でしょう？
　　　　　　　　　　　


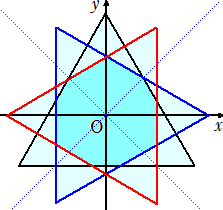
　DD++さんからのコメントです。（平成２８年１０月３１日付け）

　S₁について、これは対称に作った２つの正三角形の重なる部分が一辺 t/3 の正六角形で、
そこから高さ (1/3-1/(2))t で頂角 (2/3)π の二等辺三角形を３つ切り落とせばいいだけ
では。

　S₂について、 「重なって囲まれる」の意図がよくわからないのですが、(１)とは何が違うので
しょう？


　ＧＡＩさんからのコメントです。（平成２８年１０月３１日付け）

　言い方が難しくて．．．。　一辺が t の正三角形３つを紙で工作して、元の位置（重心は原
点、Aをy座標の正の位置）にまず一枚を敷く。次に、直線 ｙ＝ｘ で対称に移ったA’、B’、C’
を座標に持つような位置に二枚目の三角形を重ねる。（この重心も原点）
　同じく、直線 ｙ＝−ｘ で対称に移ったA”、B”、C”を座標に持つような位置に三枚目の三角
形を重ねる。（この重心も原点）

　すると、３つの三角形がずれた形でトゲトゲ星みたいな９個の三角形がとがった外周が現
れる。（３枚をのりづけして一つの図形として見て下さい。）この面積のつもりでした。
（△ABCまたは△A’B’C’または△A”B”C”'の部分といっていいのかな？）


　DD++さんからのコメントです。（平成２８年１１月１日付け）

　なるほど、重ね合わせてできる全体の図形ですか。そっちは対称に作った２つで一辺 t/3
の正三角形１２個分で、もとの正三角形でそこからはみ出ているのが一辺 (1/-1/3)t の
正三角形３個分とすればいいんじゃないでしょうか。