校の井本陽久さんの授業が紹介されていた。授業では教科書を使わないそうで、生徒の解
答が「教科書」になるという。まさに今流行のアクティブラーニングで、大変興味深く記事を
読ませていただいた。
生徒が食いつく仕掛けを作って初めて、生徒同士の議論も活発になるという考え方は、多
くの授業教材を開発し発表している筑波大学附属駒場高校にも相通じるものがある。いくつ
かその教材を眺めてみよう。
問題 △ＡＢＣにおいて、Ｂ、Ｃより対辺ＣＡ、ＡＢにそれぞれ垂線を下ろし、交点をそれぞれ
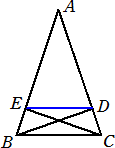Ｄ、Ｅとおく。ＢＣとＤＥが平行であるとき、ＡＢ＝ＡＣが成り立つことを証明せよ。
（解） 題意より、４点Ｂ、Ｃ、Ｄ、Ｅは同一円周上にある。よって、∠ＢＣＥ＝∠ＢＤＥ
また、ＢＣとＤＥが平行なので、∠ＢＤＥ＝∠ＣＢＤ より、 ∠ＢＣＥ＝∠ＣＢＤ
このとき、∠ＢＣＤ＝∠ＣＢＥ となり、△ＡＢＣは２等辺三角形。
よって、 ＡＢ＝ＡＣが成り立つ。 （終）
問題 正四面体Ａ-ＢＣＤの頂点および各辺の中点の計１０個の点から３点を選んで結ぶ。
このとき、合同でない２等辺三角形は何種類できるか？
（解） ６種類 （終）
