用問題である。生徒に三角形を解いてもらうとき、出題者の心理としては、正弦定理、余弦定
理が使いこなせればよいということで、なるべく辺の長さなどは、整数に設定することが多い。
よく利用される辺の長さとして、
3、5、7(辺の長さ 7 の辺の対角の大きさ: 120°)
5、8、7(辺の長さ 7 の辺の対角の大きさ: 60°)
7、8、13(辺の長さ 13 の辺の対角の大きさ: 120°)
がある。
これに対して、次の三角形の巧妙な仕掛けには、思わず唸ってしまった。
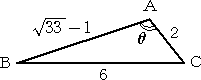
左図において、角θの大きさを求めよ。
(解) 余弦定理により、
これより、
θ=120°
(無理数がきれいに約分されるところが素晴らしい!)
