香川大学教育学部の内藤先生からご教示いただいた。
ＡＢ＝ＡＣ＝
、ＢＣ＝
である２等辺三角形ＡＢＣにおいて、辺ＡＣの中点をＭとおく。
このとき、線分ＢＭの長さを求めよ。
上図の三角形が、次のような正方形の中に埋め込まれることに気がつく方はほとんど皆無
だろう。
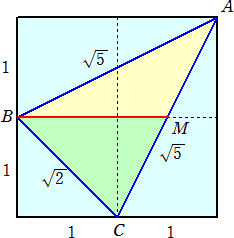
このとき、線分ＢＭの長さは、暗算で ３/２ となることが直ぐ分かる。何て、素晴らしいん
だろう！
この問題に対して、いろいろ別解を考えるのは楽しい！
（余弦定理の利用）・・・多分、多くの方が最初に思いつく解法
ＢＭ2＝ＡＢ2＋ＡＭ2−２ＡＢ・ＡＭ・ｃｏｓ∠ＢＡＭ
＝５＋５/４−２・５/２・｛（５＋５−２）/１０｝＝９/４ より、 ＢＭ＝３/２
（中線定理の利用）・・・中線定理にすぐ気がつかれた方も多いかな？
ＡＢ2＋ＢＣ2＝２（ＢＭ2＋ＡＭ2） に代入して、 ５＋２＝２（ＢＭ2＋５/４） より、
ＢＭ2＝７/２−５/４＝９/４ よって、 ＢＭ＝３/２
（座標幾何の利用）・・・Ｓ（Ｈ）さんからいただきました。（平成２８年４月２０日付け）
辺ＢＣの中点を座標軸の原点とし、ＢＣをｘ軸とすると、点Ｃを中心とし、半径
の円の方程式は、
（ｘ−１/
）2＋ｙ2＝５で、ｘ＝０を代入して、点Ａの座標（０，３/
）が求められる。よって、Ｍ（１/２
，３/２）、Ｂ（−１/，０）なので、ＢＭ2＝（３/２
）2＋（３/２）2＝９/４ より、 ＢＭ＝３/２Ｓ（Ｈ）さんは、さらに、一般的な公式も示された。（平成２８年４月２０日付け）
一般に、 AB = AC=c、BC=a とすると、BM=Sqrt[a^2/2 + c^2/4] と書ける。
（コメント） a、c が無理数だと美しくないので、この公式を用いて、すべて有理数となるもの
を探したい。ただ、答えは綺麗になるが、もはや人を感動させるような別解は存
在しなくなるような．．．雰囲気。一長一短かな？
平成２８年４月２２日付けで、Ｓ（Ｈ）さんから、ａ＝８、ｃ＝１４とすると、ＢＭ＝９とな
ることをご教示いただきました。Ｓ（Ｈ）さんに感謝します。
さらに、平成２８年４月２４日付けで、Ｓ（Ｈ）さんは、ともに整数となる例を見いださ
れた。
ａ＝１６８、ｃ＝４６、ＢＭ＝１２１ ａ＝１６８、ｃ＝８４、ＢＭ＝１２６
ａ＝１６８、ｃ＝１２４、ＢＭ＝１３４
（中点連結定理の利用） 点Ａ、Ｍから辺ＢＣに下ろした垂線の足をそれぞれＨ、Ｋとおくと、
三平方の定理より、 ＡＨ2＝５−１/２＝９/２ すなわち、 ＡＨ＝３/
よって、中点連結定理より、 ＭＫ＝３/２
したがって、 ＢＭ2＝（３/２
）2＋（−１/２）2＝９/８＋９/８＝９/４ より、ＢＭ＝３/２
（重心の性質の利用） 点Ａから辺ＢＣに下ろした垂線の足をＨ、重心をＧとおくと、
ＡＨ＝３/
から、 ＧＨ＝１/ なので、 ＢＧ2＝１ より、 ＢＧ＝１よって、 ＢＭ＝（３/２）ＢＧ＝３/２
（面積の利用）・・・Ｓ（Ｈ）さんからいただきました。（平成２８年４月２１日付け）
面積等分より、
√[(a+2c) (-a+(a+2c)/2)(-c+(a+2c)/2)(-c+(a+2c)/2)]/
=2*√[(a+c/2+m)(-a+1/2(a+c/2+m))(-(c/2)+1/2(a+c/2+m))(-m+1/2(a+c/2+m))]/
で、mを求めると、m=1/2 Sqrt[2 a^2 + c^2] を得る。
（コメント） （面積の利用）の計算は大変そう．．．。
３辺がＡＢ＝c、ＢＣ＝ａ、ＣＡ＝c の△ABCの面積は、ヘロンの公式より、
△ＡＢＣ＝（ａ/４）√（４ｃ2−ａ2）
辺ＡＣの中点Ｍについて、ＢＭ＝ｘ とおくと、ヘロンの公式より、
△ＭＢＣ＝（１/４）√｛ｃ2ａ2−（ａ2＋ｃ2/４−ｘ2）2｝
よって、 ２・（１/４）√｛ｃ2ａ2−（ａ2＋ｃ2/４−ｘ2）2｝＝（ａ/４）√（４ｃ2−ａ2） より、
４ｃ2ａ2−４（ａ2＋ｃ2/４−ｘ2）2＝４ｃ2ａ2−ａ4
すなわち、 （ａ2＋ｃ2/４−ｘ2）2＝ａ4/４ において、ａ2＋ｃ2/４−ｘ2＞０ なので、
ａ2＋ｃ2/４−ｘ2＝ａ2/２
すなわち、 ｘ2＝ａ2/２＋ｃ2/４ より、 ＢＭ＝√（ａ2/２＋ｃ2/４） を得る。
以下、工事中！
