偲偰丄偡傞側傝丅乿偺怱嫬偱丄庴尡惗偵側偭偨偮傕傝偱崱擭搙偺戝妛擖帋僙儞僞乕帋尡偺栤戣
偵挧愴偟偨偄偲巚偄傑偡丅
丂嫽枴丒娭怱傪帩偭偨栤戣傪搆慠側傞傑傑偵丏丏丏丅
悢妛嘥丒俙丂戞係栤丒丒丒惍悢偺惈幙乮晄掕曽掱幃丒値恑朄乯
乮侾乯(僀)丂晄掕曽掱幃丂俋俀倶亄侾俋俈倷亖侾丂傪枮偨偡惍悢倶丄倷偺慻偺拞偱丄倶偺愨懳抣偑嵟彫
丂丂丂丂丂偺傕偺傪媮傔傛丅
丂丂(儘)丂晄掕曽掱幃丂俋俀倶亄侾俋俈倷亖侾侽丂傪枮偨偡惍悢倶丄倷偺慻偺拞偱丄倶偺愨懳抣偑嵟
丂丂丂丂彫偺傕偺傪媮傔傛丅
乮俀乯(僀)丂俀恑朄偱侾侾侽侾侾偲昞偝傟傞悢傪係恑朄偱昞偣丅
丂丂(儘)丂師偺俇恑朄偺彫悢丂侽丏俁丂丄侽丏俁俁丂丄侽丏侽俁俁丂丄侽丏係丂丄侽丏係俁丂丄侽丏侽係俁丂偺偆
丂丂丂丂偪丄侾侽恑朄偱昞偡偲桳尷彫悢偲偟偰昞偣傞傕偺傪俁偮忋偘傛丅
乮夝乯乮侾乯(僀)丂俋俀丒侾俆亄侾俋俈丒乮亅俈乯亖侾丂側偺偱丄丂侾俋俈乮倷亄俈乯亖俋俀乮侾俆亅倶乯
丂丂丂丂俋俀偲侾俋俈偼屳偄偵慺偱丄倶丄倷偼惍悢側偺偱丄丂侾俆亅倶亖侾俋俈倠丂乮倠偼惍悢乯
丂丂丂丂丂傛偭偰丄丂倶亖侾俆亅侾俋俈倠丂偱丄倶偺愨懳抣偑嵟彫偲側傞偺偼丄倠亖侽偺偲偒
丂丂丂丂埲忋偐傜丄媮傔傞倶偺抣偼丄丂倶亖侾俆
丂丂丂丂偙偺偲偒丄丂倷亖亅俈
丂乮儘乯丂乮僀乯傛傝丄俋俀丒侾俆侽亄侾俋俈丒乮亅俈侽乯亖侾侽丂側偺偱丄侾俋俈乮倷亄俈侽乯亖俋俀乮侾俆侽亅倶乯
丂丂丂丂俋俀偲侾俋俈偼屳偄偵慺偱丄倶丄倷偼惍悢側偺偱丄丂侾俆侽亅倶亖侾俋俈倠丂乮倠偼惍悢乯
丂丂丂丂丂傛偭偰丄丂倶亖侾俆侽亅侾俋俈倠丂偱丄倶偺愨懳抣偑嵟彫偲側傞偺偼丄倠亖侾偺偲偒
丂丂丂丂埲忋偐傜丄媮傔傞倶偺抣偼丄丂倶亖亅係俈
丂丂丂丂偙偺偲偒丄丂倷亖俀俀
乮俀乯(僀)丂俀恑朄偱侾侾侽侾侾偲昞偝傟傞悢偼丄
丂丂丂丂丂侾侾侽侾侾亖侾丒俀4亄侾丒俀3亄侽丒俀2亄侾丒俀亄侾亖侾丒係2亄(俀亄侽乯丒係亄乮俀亄侾乯
丂丂丂丂偲昞偝傟傞偺偱丄係恑朄偱昞偡偲丄丂侾俀俁丂偲彂偗傞丅
丂(儘)丂師偺俇恑朄偺彫悢丂侽丏俁丂丄侽丏俁俁丂丄侽丏侽俁俁丂丄侽丏係丂丄侽丏係俁丂侽丏侽係俁傪侾侽恑
丂丂丂朄偱昞偡偲丄
丂丂丂侽丏俁亖俁/俇亖侾/俀亖侽丏俆丂乮桳尷彫悢乯
丂丂丂侽丏俁俁亖俁/俇亄俁/俁俇亖侾/俀亄侾/侾俀亖侽丏俆亄侽丏侽俉俁俁俁丒丒丒丂乮柍尷彫悢乯
丂丂丂侽丏侽俁俁亖俁/俁俇亄俁/俀侾俇亖侾/侾俀亄侾/俈俀亖俈/俈俀亖侽丏侽俋俈俀俀俀丒丒丒丂乮柍尷彫悢乯
丂丂丂侽丏係亖係/俇亖俀/俁亖侽丏俇俇俇丒丒丒丂乮柍尷彫悢乯
丂丂丂侽丏係俁亖係/俇亄俁/俁俇亖俀/俁亄侾/侾俀亖俋/侾俀亖俁/係亖侽丏俈俆丂乮桳尷彫悢乯
丂丂丂侽丏侽係俁亖係/俁俇亄俁/俀侾俇亖侾/俋亄侾/俈俀亖侾/俉亖侽丏侾俀俆丂乮桳尷彫悢乯
丂丂埲忋偐傜丄媮傔傞傕偺偼丄侽丏俁丂丄侽丏係俁丂侽丏侽係俁
乮僐儊儞僩乯丂乮侾乯偼丄偄傠偄傠側夝朄偑峫偊傜傟傞丅堦斒偵偼屳彍朄傪梡偄傞偺偩傠偆丅偨偩丄
丂丂丂丂丂丂偙偺庤偺栤戣偼丄摿庩夝傪扵偟偨曽偑夝摎偼妝偱偁傞丅乮俀乯偼値恑朄偺堄枴傪棟
丂丂丂丂丂丂夝偟偰偄傟偽梕堈側栤戣偩傠偆丅
乮捛婰乯丂暯惉俀俉擭俀寧俀侽擔晅偗
悢妛嘥丒俙丂戞俆栤丒丒丒恾宍偺惈幙乮墌偵撪愙偡傞巐妏宍丄儊僱儔僂僗偺掕棟丄僠僃僶偺掕棟丄曽傋偒偺掕棟乯
丂巐妏宍ABCD偵偍偄偰丄AB亖係丄BC亖俀丄DA亖DC偱偁傝丄係偮偺捀揰A丄B丄C丄D偼摨堦墌
廃忋偵偁傞丅懳妏慄AC偲懳妏慄BD偺岎揰傪E丄慄暘AD傪俀丗俁偺斾偵撪暘偡傞揰傪F丄捈慄
FE偲捈慄DC偺岎揰傪G偲偡傞丅師偺栤偄偵摎偊傛丅
丂丂丂
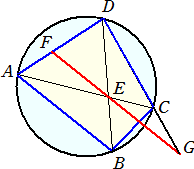
丂佢ABC偺戝偒偝偑曄壔偡傞偲偒丄巐妏宍ABCD偺奜愙墌偺戝偒偝傕曄壔偡傞偙偲偵拲堄偡傞
偲丄佢ABC偺戝偒偝偑偄偔傜偱偁偭偰傕丄佢DAC偲戝偒偝偑摍偟偄妏偱丄佢DCA偲佢DBC埲奜偺
妏傪媮傔傛丅
丂偙偺偲偒丄EC/AE傪媮傔傛丅師偵丄仮ACD偲捈慄FE偵拝栚偟偰丄GC/DG傪媮傔傛丅
乮侾乯丂捈慄AB偑揰G傪捠傞応崌偵偮偄偰峫偊傞丅
丂丂偙偺偲偒丄仮AGD偺曈AG忋偵揰B偑偁傞偙偲偐傜丄BG傪媮傔傛丅傑偨丄捈慄AB偲捈慄DC
丂偑揰G偱岎傢傝丄係揰A丄B丄C丄D偼摨堦墌廃忋偵偁傞偙偲偐傜丄DC傪媮傔傛丅
乮俀乯丂巐妏宍ABCD偺奜愙墌偺敿宎偑嵟彫偲側傞応崌偵偮偄偰峫偊傞丅
丂丂偙偺偲偒丄巐妏宍ABCD偺奜愙墌偺捈宎偍傛傃佢BAC偺戝偒偝傪媮傔傛丅傑偨丄捈慄FE
丂偲捈慄AB偺岎揰傪H偲偡傞偲偒丄AH傪媮傔傛丅
乮夝乯丂恾傛傝丄佢DAC亖佢DCA亖佢DBC亖佢DBA丂偱偁傞丅傛偭偰丄慄暘BE偼佢ABC偺俀摍
丂丂暘慄偱偁傞偺偱丄丂EC/AE亖BC/BA亖俀/係亖侾/俀
丂丂傑偨丄儊僱儔僂僗偺掕棟傛傝丄乮AF/FD乯乮DG/GC乯乮CE/EA乯亖侾丂偑惉傝棫偮偺偱丄
丂丂丂乮俀/俁乯乮DG/GC乯乮侾/俀乯亖侾丂傛傝丄丂GC/DG亖侾/俁
乮侾乯丂仮AGD偵偍偄偰丄僠僃僶偺掕棟傛傝丄丂乮係/BG乯乮侾/俀乯乮俁/俀乯亖侾丂偑惉傝棫偮偺偱丄
丂丂丂俛俧亖俁丂偲側傞丅傑偨丄GC亖倶丂偲偍偔偲丄DG亖俁倶丂偱丄曽傋偒偺掕棟傛傝丄
丂丂丂俁丒俈亖倶丒俁倶丂傛傝丄丂倶亖
乮俀乯丂巐妏宍ABCD偺奜愙墌偼仮ABC偺奜愙墌偱傕偁傞丅惓尫掕棟傛傝丄奜愙墌偺敿宎傪
丂丂俼偲偡傞偲丄丂俀俼亖係/sin佢ACB丂側偺偱丄俼偑嵟彫偲側傞偺偼丄sin佢ACB亖侾丂懄偪丄
丂丂佢ACB亖俋侽亱傛傝丄AB偑奜愙墌偺捈宎偺偲偒偱偁傞丅
丂丂丂傛偭偰丄丂巐妏宍ABCD偺奜愙墌偺捈宎偼丄丂俀俼亖係丂偱丄佢BAC亖俁侽亱偱偁傞丅
丂丂慄暘BE偼佢ABC偺俀摍暘慄偱偁傞偺偱丄佢ABD亖佢CBD亖俁侽亱
丂丂傛偭偰丄丂AD亖DC亖BC亖俀丂偲側傞丅
丂丂偝傜偵丄嶖妏偑摍偟偄偺偱丄丂AB乤DC丂偑惉傝棫偮偺偱丄丂仮HAE佷仮GCE
丂丂傛偭偰丄丂AH/GC亖俀/侾丂偱丄丂GC亖DC/俀亖侾丂傛傝丄丂AH亖俀丂丂乮廔乯
乮僐儊儞僩乯丂乮俀乯偑彮偟峫偊偝偣傞栤戣偱偡偹両怴孹岦偺栤戣偩偲巚偄傑偡丅
乮捛婰乯丂暯惉俀俉擭俀寧俀侾擔晅偗
悢妛嘥丒俙丂戞俁栤丒丒丒応崌偺悢偲妋棪乮忦審晅偒妋棪乯
丂愒媴係屄丄惵媴俁屄丄敀媴俆屄丄崌寁侾俀屄偺媴偑偁傞丅偙傟傜侾俀屄偺媴傪戃偺拞偵擖傟丄
偙偺戃偐傜A偝傫偑傑偢侾屄庢傝弌偟丄偦偺媴傪傕偲偵栠偝偢偵懕偄偰B偝傫偑侾屄庢傝弌偡丅
乮侾乯丂A偝傫偲B偝傫偑庢傝弌偟偨俀屄偺媴偺拞偵丄愒媴偐惵媴偑彮側偔偲傕侾娷傑傟偰偄傞妋
丂丂棪傪媮傔傛丅
乮俀乯丂A偝傫偑愒媴傪庢傝弌偟丄偐偮B偝傫偑敀媴傪庢傝弌偡妋棪傪媮傔傛丅偙傟傛傝丄A偝傫
丂丂偑庢傝弌偟偨媴偑愒媴偱偁偭偨偲偒丄B偝傫偑庢傝弌偟偨媴偑敀媴偱偁傞忦審晅偒妋棪傪
丂丂媮傔傛丅
乮俁乯丂A偝傫偼侾媴庢傝弌偟偨偺偪丄偦偺怓傪尒偢偵億働僢僩偺拞偵偟傑偭偨丅B偝傫偑庢傝弌偟
丂丂偨媴偑敀媴偱偁傞偙偲偑傢偐偭偨偲偒丄A偝傫偑庢傝弌偟偨媴傕敀媴偱偁偭偨忦審晅偒妋
丂丂棪傪媮傔偨偄丅
丂丂丂A偝傫偑愒媴傪庢傝弌偟丄偐偮B偝傫偑敀媴傪庢傝弌偡妋棪偼乮俀乯傛傝摼傜傟傞丅A偝傫偑
丂丂惵媴傪庢傝弌偟丄偐偮B偝傫偑敀媴傪庢傝弌偡妋棪傪媮傔傛丅
丂丂丂摨條偵丄A偝傫偑敀媴傪庢傝弌偟丄偐偮B偝傫偑敀媴傪庢傝弌偡妋棪傪媮傔傞偙偲偑偱偒丄
丂丂偙傟傜偺帠徾偼屳偄偵攔斀偱偁傞偙偲傪梡偄偰丄B偝傫偑敀媴傪庢傝弌偡妋棪傪媮傔傛丅
丂丂丂埲忋傪梡偄偰丄強梫偺忦審晅偒妋棪傪媮傔傛丅
乮夝乯乮侾乯丂A偝傫偲B偝傫偑庢傝弌偟偨俀屄偺媴偑偡傋偰敀媴偱偁傞妋棪偼丄
丂丂丂丂丂乮俆/侾俀乯乮係/侾侾乯亖俆/俁俁丂傛傝丄媮傔傞妋棪偼丄侾亅俆/俁俁亖俀俉/俁俁
乮俀乯丂A偝傫偑愒媴傪庢傝弌偟丄偐偮B偝傫偑敀媴傪庢傝弌偡妋棪偼丄乮係/侾俀乯乮俆/侾侾乯亖俆/俁俁
丂丂A偝傫偑庢傝弌偟偨媴偑愒媴偱偁偭偨偲偒丄B偝傫偑庢傝弌偟偨媴偑敀媴偱偁傞忦審晅偒
丂妋棪偼丄
丂丂丂丂丂丂丂乮俆/俁俁乯/乮係/侾俀乯亖俆/侾侾
乮俁乯丂A偝傫偑愒媴傪庢傝弌偟丄偐偮B偝傫偑敀媴傪庢傝弌偡妋棪偼丄乮係/侾俀乯乮俆/侾侾乯亖俆/俁俁
丂丂A偝傫偑惵媴傪庢傝弌偟丄偐偮B偝傫偑敀媴傪庢傝弌偡妋棪偼丄乮俁/侾俀乯乮俆/侾侾乯亖俆/係係
丂丂A偝傫偑敀媴傪庢傝弌偟丄偐偮B偝傫偑敀媴傪庢傝弌偡妋棪偼丄乮俆/侾俀乯乮係/侾侾乯亖俆/俁俁
丂丂傛偭偰丄B偝傫偑敀媴傪庢傝弌偡妋棪偼丄丂俆/俁俁亄俆/係係亄俆/俁俁亖俆/侾俀
丂埲忋偐傜丄B偝傫偑庢傝弌偟偨媴偑敀媴偱偁傞偙偲偑傢偐偭偨偲偒丄A偝傫偑庢傝弌偟偨媴傕
敀媴偱偁偭偨忦審晅偒妋棪偼丄
丂丂丂丂丂丂乮俆/俁俁乯/乮俆/侾俀乯亖係/侾侾
乮僐儊儞僩乯丂摫擖偵廬偭偰寁嶼偡傟偽梕堈丅偨偩丄偙偙傑偱挌擩側摫擖偼昁梫側偺偩傠偆偐丠
悢妛嘦丒悢妛俛丂戞俁栤丒丒丒悢楍乮孮悢楍乯
丂恀暘悢傪暘曣偺彫偝偄弴偵丄暘曣偑摨偠応崌偵偼暘巕偺彫偝偄弴偵暲傋偰偱偒傞悢楍
丂侾/俀丆侾/俁丆俀/俁丆侾/係丆俀/係丆俁/係丆侾/俆丆丒丒丒
傪乷倎値乸偲偡傞丅恀暘悢偲偼丄暘巕偲暘曣偑偲傕偵帺慠悢偱丄暘巕偑暘曣傛傝彫偝偄暘悢偺偙
偲偱偁傝丄忋偺悢楍偱偼丄栺暘偱偒傞宍偺暘悢傕娷傔偰暲傋偰偄傞丅埲壓偺栤戣偵暘悢宍偱
夝摎偡傞応崌偼丄偦傟埲忋栺暘偱偒側偄宍偱摎偊傛丅
乮侾乯丂倎15 傪媮傔傛丅傑偨丄暘曣偵弶傔偰俉偑尰傟傞偺偼壗斣栚偺崁偐丅
乮俀乯丂倠傪俀埲忋偺帺慠悢偲偡傞丅悢楍乷倎値乸偵偍偄偰丄侾/倠偑弶傔偰尰傟傞崁傪戞俵倠崁偲偟丄
丂丂乮倠亅侾乯/倠偑弶傔偰尰傟傞崁傪戞俶倠崁偲偡傞偲偒丄俵倠丄俶倠傪倠偺俀師幃偱昞偣丅
丂丂丂傑偨丄倎104 傪媮傔傛丅
乮俁乯丂倠傪俀埲忋偺帺慠悢偲偡傞丅悢楍乷倎値乸偺戞俵倠崁偐傜戞俶倠崁傑偱偺榓傪媮傔傛丅傑偨丄
丂丂悢楍乷倎値乸偺弶崁偐傜戞俶倠崁傑偱偺榓傪媮傔傛丅
丂丂丂偝傜偵丄儼n=1乣103 倎値 傪媮傔傛丅
乮夝乯乮侾乯丂戞侾孮丗侾/俀
丂丂丂丂丂丂戞俀孮丗侾/俁丆俀/俁
丂丂丂丂丂丂戞俁孮丗侾/係丆俀/係丆俁/係
丂丂丂丂丂丂丂丒丒丒丒丒丒丒丒丒丒丒丒丒
丂丂丂偲峫偊傞丅戞値孮偺弶崁偼丄侾/乮値亄侾乯丂偱丄崁悢偼丄値丂偱偁傞偺偱丄
丂丂丂丂侾亄俀亄俁亄係亄俆亖侾俆丂傛傝丄倎15 偼丄戞俆孮偺枛崁偱偁傞丅傛偭偰丄倎15亖俆/俇
丂丂暘曣偵弶傔偰俉偑尰傟傞偺偼戞俈孮偺弶崁側偺偱丄
丂丂丂丂侾亄俀亄俁亄係亄俆亄俇亄侾亖俀俀乮斣栚乯
乮俀乯丂俵倠亖侾亄俀亄俁亄丒丒丒亄乮倠亅俀乯亄侾亖乮倠2亅俁倠亄係乯/俀
丂丂丂俶倠亖侾亄俀亄俁亄丒丒丒亄乮倠亅侾乯亖乮倠2亅倠乯/俀
丂丂乮倠2亅俁倠亄係乯/俀亝侾侽係丂傪枮偨偡嵟戝偺帺慠悢偼丄倠亖侾俆
丂丂傛偭偰丄倎104 偼丄戞侾係孮偺侾俁斣栚偺悢側偺偱丄丂侾俁/侾俆
乮俁乯丂悢楍乷倎値乸偺戞俵倠崁偐傜戞俶倠崁傑偱偺榓偼丄弶崁侾/倠丄枛崁乮倠亅侾乯/倠丄崁悢倠亅侾
丂丂偺摍嵎悢楍偺榓側偺偱丄
丂丂丂乮倠亅侾乯乮侾/倠亄乮倠亅侾乯/倠乯/俀亖乮倠亅侾乯/俀
丂丂傑偨丄悢楍乷倎値乸偺弶崁偐傜戞俶倠崁傑偱偺榓偼丄儼値=2乣倠 乮値亅侾乯/俀亖乮倠2亅倠乯/係
丂丂倎103 偼丄戞侾係孮偺侾俀斣栚偺悢側偺偱丄
丂丂儼n=1乣103 倎値亖儼値=2乣15 乮値亅侾乯/俀亅侾俁/侾俆亅侾係/侾俆亖侾侽俆/俀亅俋/俆亖俆侽俈/侾侽
乮僐儊儞僩乯丂俀侽侾侽擭搙埲棃偺孮悢楍偺栤戣偱丄寢峔嵶偐偄婥尛偄偑昁梫側栤戣偱偡偹丅
丂丂埲壓丄岺帠拞両
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
