長年証明できない問題があります。みなさんの力で解いていただきたいと思います。

　復素数平面上に、同一直線上にない３点 α₁、β₁、γ₁ が正の回転の順にあり、三角形
を作っているとする。

　そこで、α₁ を γ₁ を中心に正の方向へ角 ａｒｇ（β₁−γ₁）/（α₁−γ₁）だけ動かした
点を α₂ とする。

　つまり、式にすると、　α₂＝｜α₁−γ₁｜/｜β₁−γ₁｜・（β₁−γ₁）＋γ₁

　同様にして、β₂＝｜β₁−α₁｜/｜γ₁−α₁｜・（γ₁−α₁）＋α₁

　　　　　　　　γ₂＝｜γ₁−β₁｜/｜α₁−β₁｜・（α₁−β₁）＋β₁

を得る。順次、この操作を繰り返し、α₃β₃γ₃、・・・、α_nβ_nγ_n を得る。

　n→∞ のとき、三角形 α_nβ_nγ_n は正三角形になる。

　計算が複雑になり、お手上げです。エレガントな解答はないでしょうか。


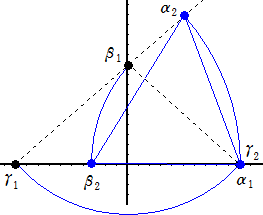
（コメント）　問題の意味を把握するため、α₁＝１、β₁＝ｉ、γ₁＝−１ として、α₂、β₂、γ₂
　　　　　　を作図してみた。