下図の直角三角形において、３辺の長さ ａ、ｂ、ｃ がすべて整数のとき、内接円の半径 ｒ
も整数となる。
　　　　　

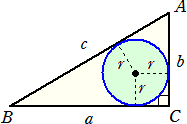
　実際に、　ｃ＝ａ−ｒ＋ｂ−ｒ　より、　ｒ＝（ａ＋ｂ−ｃ）/２

　ここで、　ａ²＋ｂ²＝ｃ²　において、起こりうる場合の組（ａ，ｂ，ｃ）は、

　（偶数，偶数，偶数）、（偶数，奇数，奇数）、（奇数，偶数，奇数）、（奇数，奇数，偶数）

であるが、何れにしても　ａ＋ｂ−ｃ は偶数となり、　ｒ＝（ａ＋ｂ−ｃ）/２　は整数となる。

　さらに、　ａ²＋ｂ²＝ｃ²＝（ａ＋ｂ−２ｒ）²　より、　ａｂ−２ｒ（ａ＋ｂ）＋２ｒ²＝０　なので、

　（ａ−２ｒ）（ｂ−２ｒ）＝２ｒ²　より、起こりえる場合は、

　（ａ−２ｒ，ｂ−２ｒ）＝（１，２ｒ²）、（２，ｒ²）、（ｒ，２ｒ）、・・・　など。

　（ａ，ｂ）＝（２ｒ＋１，２ｒ²＋２ｒ）、（２ｒ＋２，ｒ²＋２ｒ）、（３ｒ，４ｒ）、・・・

より、内接円の半径が ｒ のときの直角を挟む２辺の長さが得られる。


　よおすけさんからのコメントです。（平成２７年７月２９日付け）

　a=3、b=4、c=5のとき、r=1となるから、逆に、(a,b)=(2r+1,2r²+2r)、(2r+2,r²+2r)、(3r,4r)　に

r=1をそれぞれ代入すれば、(a,b)=(3,4)、(4,3)、(3,4)　となり、元の(a,b)と一致の組は存在する。

ところが、a=20、b=21、c=29のとき、r=6　となるが、r=6を

(a,b)=(2r+1,2r²+2r)、(2r+2,r²+2r)、(3r,4r)　にそれぞれ代入した場合、

　(a,b)=(13,84)、(14,48)、(18,24)

となり、元の(a,b)と一致しない。


（コメント）　r=6　なので、　（ａ−１２）（ｂ−１２）＝７２　から、

　（ａ−１２，ｂ−１２）＝（８，９）、・・・・　より、　（ａ，ｂ）＝（２０，２１）、・・・

　DD++さんからも平成２７年７月２９日付けでご指摘頂いたが、ｒは素数とは言っていないの
で、（ａ−２ｒ）（ｂ−２ｒ）＝２ｒ²　の解は、（２ｒ＋１，２ｒ²＋２ｒ）、（２ｒ＋２，ｒ²＋２ｒ）、（３ｒ，４ｒ）
以外にもたくさん存在する。