分数 23/67 と 33/97 の大小を<暗算で>判定せよ。
「<暗算で>判定せよ。」という条件がなければ、当然電卓を使って、
23/67=0.3432835・・・ 、33/97=0.3402061・・・
なので、 23/67 > 33/97 と分かるし、多少計算の煩雑さを我慢して、
23/67 − 33/97
=(23・97−33・67)/(67・97)=(2231−2211)/(67・97)=20/(67・97)>0
から、 23/67 > 33/97 と判定するのが常道だろう。
これに対して、「<暗算で>判定せよ。」ということなので、次のように考えてみた。
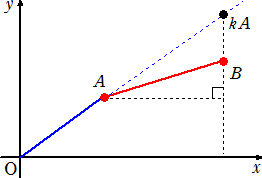
座標平面上に、3点O(0,0)、A(67,23)、B(97,33)をとる。
このとき、線分ABの傾きmは、m=(33−23)/(97−67)=1/3 (← 暗算!)
ところで、 線分OAの傾きnは、n=23/67>23/69=m (← 暗算!)
したがって、 23/67 > 33/97 であることが分かる。
(コメント) 自信はないが、これが最善と思う。別にもっといい判定法があれば、ご教示くだ
さい。
らすかるさんからのコメントです。(平成27年4月13日付け)
それぞれ3倍して1を引くと、
(23/67)×3-1=69/67-1=2/67 (← 23×3-67=2 は暗算)
(33/97)×3-1=99/97-1=2/97 (← 33×3-97=2 は暗算)
だから23/67の方が大きい。
# いくつか書いては消し書いては消ししましたが、最良と思われる一つだけ残しました。
(コメント) なるほど!「3倍して1を引く」と、ともに分子が同じ数「2」になるんですね!感動
的ですね。
DD++さんからのコメントです。(平成27年4月13日付け)
私がすぐに思いついたのは、
23/67 の逆数は、 67/23 = 3 - 2/23
33/97 の逆数は、 97/33 = 3 - 2/33
よって、 67/23 < 97/33 だから、 23/67 > 33/97
(コメント) らすかるさんの発想「3倍して1を引く」と同義ですね!なるほどです。
(追記) 平成28年1月17日付け
実は、冒頭の問題は、一松 信先生出題のものであるが、最近、一松 信先生から解答
をいただいて、よく見ると、DD++さんの解答と同じでした!
よおすけさんからのコメントです。(平成27年4月13日付け)
アバウトにやれば、
67は四捨五入で約70、97は四捨五入で約100だから、23に100、33に70をかけてみます。
23×100=2300、33×70=2310
これが、2数を通分したときの仮の分子の値になります。
求める各分子の値は、それぞれ23×3、33×3少ないですから、
23×97=2231、33×67=2211 となり、 23/67>33/97。
tetsuさんからのコメントです。(平成27年4月14日付け)
23/67 は、1/3=23/69 の分母を2小さくしたもの。
33/97 は、1/3=33/99 の分母をやはり2小さくしたもの。
後者のほうが「分母が小さくなっている率」が少ないことになるので、前者のほうが大きい
と思いました。
(追記) 共互除法と題して、DD++さんからの投稿です。(平成27年4月16日付け)
「分数の大小」からの発展で、ちょっと面白い計算を思いついたので投稿します。
比の異なる非負整数の組を2つ用意します。例えば、(38,61) と (33,53) を用意します。
これを左の数字同士、右の数字同士で割り算し、商が小さい方を共通商とします。
余り(片方は割る数より大きくなる場合もある)を出し、互除法のように計算していきます。
(38,61) ÷ (33,53) = 1 あまり (5,8)
(33,53) ÷ (5,8) = 6 あまり (3,5)
(5,8) ÷ (3,5) = 1 あまり (2,3)
(3,5) ÷ (2,3) = 1 あまり (1,2)
(2,3) ÷ (1,2) = 1 あまり (1,1)
(1,2) ÷ (1,1) = 1 あまり (0,1)
すると、 (38,61)、 (33,53)、 (5,8)、 (3,5)、 (2,3)、 (1,2)、 (1,1)、 (0,1) というペアの
列ができます。これを (分子,分母) と思って分数列にします。
38/61, 33/53, 5/8, 3/5, 2/3, 1/2, 1/1, 0/1
この分数列は以下のような性質があります。
2番目の 33/53 はそれまでの2数で最小
3番目の 5/8 はそれまでの3数で最大
4番目の 3/5 はそれまでの4数で最小
5番目の 2/3 はそれまでの5数で最大
6番目の 1/2 はそれまでの6数で最小
7番目の 1/1 はそれまでの7数で最大
8番目の 0/1 はそれまでの8数で最小
この最大と最小が交互に現れる性質はどんな2組の数からスタートしても発生することが
証明できます。最初の2数のどちらが大きいかで2番目が最小から始まる場合と最大から
始まるパターンの違いはありますが...。
つまり、逆に利用すると、38/61 と 33/53 の大小がわからない場合に、この計算をし、8番
目の 0/1 が明らかに最小なので、2番目はそこまでで最小つまり1番目より小さいと判断す
ることもできます。(NGワード:普通に割り算した方が早い)
とりあえず「なんか面白い性質見つけた」段階でしかありませんが、何かに利用できないか
なあ。
