・　挑発的な問題　　　　　　　　　　　　　　　　　　　Ｓ．Ｈ氏

　朝刊を何とはなしに眺めていたら、広告欄に「この問題を３０秒で解けますか？」という数学
の問題が載っていた。ちょっと刺激的なタイトルだったので、考えてみることにした。

　問題は、次のようなものである。

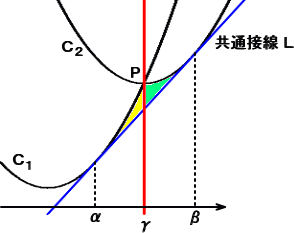
（１）　放物線 Ｙ＝Ｘ² を平行移動させた、２つの放物線 Ｃ₁、Ｃ₂ が、点Ｐで交わっている。
　　このとき、Ｃ₁、Ｃ₂ とその共通接線 Ｌ とで囲まれる部分の面積は、点Ｐを通りＹ軸に平行な
　　直線で２等分されることを示せ。
　　　　　　　　　　　　　　　　　　　　
（２）　１、１、２、２、３、３、４、４ の８個の数字を並べてできる８桁の数の中に、平方数はある
　　か？

　正直に告白すると、とても３０秒で、２つの問題を解くことはできなかった。しかし、十分数学
の楽しさを味わうことができた。広告のコピーに、「心に広がる数学の世界を！」とあるように、
このような問題で１年間鍛えられたら学校教育における数学のイメージが根底から覆るような
ショックを受けることは間違いない。私が高校生の頃、このような学びの場がなかったことを残
念に思う。私なりに、上の問題に対して、次のように解いてみた。

（１）に対する私の解答 ：

　Ｃ₁ ： Ｙ＝Ｘ²＋ａＸ＋ｂ　　Ｃ₂ ： Ｙ＝Ｘ²＋ｃＸ＋ｄ　　Ｌ ： Ｙ＝ｍＸ＋ｎ　とする。上図のように、
接点のＸ座標を α、β とし、点ＰのＸ座標を γ とする。このとき、γ は α、β の平均である。

　実際に、Ｃ₁−Ｃ₂ より、（ａ−ｃ）γ＝ｄ−ｂ　が成り立ち、また、
　　　　　Ｘ²＋ａＸ＋ｂ−（ｍＸ＋ｎ）＝（Ｘ−α）² から、ａ−ｍ＝−２α、ｂ−ｎ＝α²
　　　　　Ｘ²＋ｃＸ＋ｄ−（ｍＸ＋ｎ）＝（Ｘ−β）² から、ｃ−ｍ＝−２β、ｄ−ｎ＝β²
から、ａ−ｃ＝２（β−α）、ｄ−ｂ＝β²−α²　となる。これらを最初の式に代入して、
　　　　　　　　　　　　　　２（β−α）γ＝β²−α²
　α≠β　としてよいので、γ＝（α＋β）/２　すなわち、γ−α＝β−γ　が成り立つ。

ところで、上図の黄色い部分の面積は、
　　　　　　
同様にして、上図の黄緑部分の面積は、
　　　　　　

このとき、γ−α＝β−γ　なので、両者は等しい。よって、題意は示された。

（注）　この問題のポイントは、「γ は、α、β の平均である」ことと、「放物線と直線で囲まれ
　　　た部分の面積は、それらの交点のＸ座標のみによって定まる」ことの２点であろう。積分
　　　を用いないで、図形的に示すことができないか、いろいろ実験してみたが、上手い解答
　　　が思い浮かばなかった。３０秒で解けるということなので、多分もっとエレガントな解答が
　　　あるのだろう。

　（追記）　平成２１年３月１９日付けで、ＨＮ「凡人」さんから、当ＨＰの掲示板「出会いの泉」に
　　　　　投稿がありました。

　　　以下のように考えると、３０秒以内ではないでしょうか？
　　Ｃ₁ ： Ｙ＝Ｆ（Ｘ）　　Ｃ₂ ： Ｙ＝Ｇ（Ｘ）　　Ｌ ： Ｙ＝Ｈ（Ｘ）　とする。このとき、
　Ｆ（Ｘ）−Ｈ（Ｘ）＝（Ｘ−α）²　、Ｇ（Ｘ）−Ｈ（Ｘ）＝（Ｘ−β）² は直線 Ｘ＝γに関して対称なので、
　　　　　
　これにより、題意は示された。

　（コメント）　本解とほぼ同じ発想ですが、計算していない分「速攻」ですね！「放物線−直線」
　　　　　　　が左右対称な放物線であることに気がつくことが大切なのでしょう。「凡人」さんに
　　　　　　　感謝します。

（２）に対する私の解答 ：

　８桁の数は、Ｎ＝ ａ・１０⁷＋ｂ・１０⁶＋ｃ・１０⁵＋ｄ・１０⁴＋ｅ・１０³＋ｆ・１０²＋ｇ・１０＋ｈ　
　　　　　　　　　　　　　（ａ、ｂ、ｃ、ｄ、ｅ、ｆ、ｇ、ｈ　は、１、１、２、２、３、３、４、４　の何れか）
と表される。
　任意の自然数 ｋ に対して、１０^ｋ ≡ １　（ｍｏｄ　３）　で、これは、１０^ｋ−１ が ３ で割り切れ
ることを意味する。このとき、
　Ｎ≡ａ＋ｂ＋ｃ＋ｄ＋ｅ＋ｆ＋ｇ＋ｈ＝１＋１＋２＋２＋３＋３＋４＋４＝２０≡２　（ｍｏｄ　３）
なので、Ｎを ３ で割った余りは、２ となる。

　いま、Ｎが自然数の平方であると仮定する。自然数を ３ で割った余りは、０、１、２ の何れ
かなので、Ｎを ３ で割った余りは、０、１ の何れかになる。これは、Ｎを ３ で割った余りが、２
であることに矛盾する。

　したがって、１、１、２、２、３、３、４、４ の８個の数字を並べてできる８桁の数の中に、平方数
は存在しえない。

（注）　このような整数論もどきの議論は、学校教育ではあまり深く教えられない分野に入る
　　　が、数学を究めるためには、必ずマスターしなければならない基本的技法だと思う。


（追記）　「挑発的な問題２」として、当ＨＰがいつもお世話になっているＨＮ「よおすけ」さんか
　　　　ら問題を頂いた。（平成２６年８月４日付け）

　次の問題を３０秒以内で答えろ、と言われたら、多くの方が戸惑うでしょう。

　ａ の３次方程式 ａ³-1=0 の３つの解を ｘ、ｙ、ｚ とするとき、
ｘ³(ｙ-ｚ)＋ｙ³(ｚ-ｘ)＋ｚ³(ｘ-ｙ) の値を求めよ。

　多分、与式をまともに因数分解するだけで１０分はかかるでしょう。（→個人差あり）
さらに、解と係数との関係の記述も書いてしまうと、まず３０秒では終わらないでしょう。

　僕も最初はそう思っていましたが、以下の方法でも解けることが判明しました。

（解）　ｘ、ｙ、ｚ は、ａ³-1=0 の解だから、　ｘ³=ｙ³=ｚ³=１　より、与式=(ｙ-ｚ)＋(ｚ-ｘ)＋(ｘ-ｙ)=0

※　これなら、３０秒以内に解けると思われますが、他の方法もあるかもしれません。


（コメント）　この問題を見て、上記の解しか思いつきませんでした！因数分解とか解と係数
　　　　　　の関係とかやろうとも思いませんでした。

　因数分解すると、（ｘ−ｙ）（ｘ−ｚ）（ｙ−ｚ）（ｘ＋ｙ＋ｚ）となり、ｘ＋ｙ＋ｚ＝０　から答えを導くの
はかなりの遠回りですね！