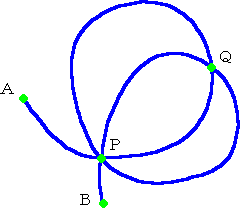
たして、どのような性質を持つものが、「交点」と認
識されるのであろうか?
左図において、点A、B を端点といい、点P、Q
を交点という。これら以外の点を、一般点という。
端点とは、その点を中心として、半径の十分小
さい円を描いたとき、その円が曲線を1回だけ切
るときをいう。
交点とは、その点を中心として、半径の十分小
さい円を描いたとき、その円が曲線を3回以上切
るときをいう。
・ 全ての点が交点である曲線 S.H氏
 |
直感的に、我々は、交点をイメージできるが、は たして、どのような性質を持つものが、「交点」と認 識されるのであろうか? 左図において、点A、B を端点といい、点P、Q を交点という。これら以外の点を、一般点という。 端点とは、その点を中心として、半径の十分小 さい円を描いたとき、その円が曲線を1回だけ切 るときをいう。 交点とは、その点を中心として、半径の十分小 さい円を描いたとき、その円が曲線を3回以上切 るときをいう。 |
一般点とは、その点を中心として半径の十分小さい円を描いたとき、その円が曲線を2回
切るときをいう。
常識的に考えて、交点だけからなる曲線は存在しないように思える。
この常識を否定的に解決したのが、シェルピンスキー(1915年)である。その曲線は、
次のように構成される。
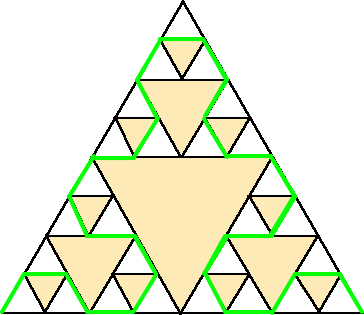 |
正三角形の各辺の中点を結ん で、合同な正三角形に分割する。 真ん中の正三角形を除いて、 さらに、正三角形の各辺の中点 を結んで、合同な正三角形に分 割する。このような分割を、無限 に続ける。 このときできる曲線が、交点ば かりからなる曲線の例を与える らしい。ただし、最初の三角形の 頂点は省いて考える。 左図は、最初の正三角形の分 割を、3回繰り返した図である。 緑色の線が、該当の曲線であ るが、これが所要の性質を本当 に持つのかどうか、イメージする ことは難しい。 |
上の操作で、曲線のことを考えず、ただひたすら分割を繰り返して、真ん中の正三角形
を除く操作を続けると、フラクタル図形では有名な、「シェルピンスキーのギャスケット」が
得られる。
どちらも、我々凡人には計り知れない「妖しい図形」である。
(参考文献:E.P.ノースロップ 著 松井政太郎 訳 ふしぎな数学(みすず書房)
高安秀樹 著 フラクタル(朝倉書店))
