・　比例式の計算　　　　　　　　　　　　　　　Ｓ．Ｈ氏

比例式		を満たす実数 Ａ、Ｂ を求めてみよう。
分母を払って、　　 （１＋Ａ）Ａ＝（１＋Ｂ）Ｂ 右辺を左辺に移項して、因数分解すると、 　　　　　　　　　　　　（Ａ−Ｂ)(Ａ＋Ｂ＋１）＝０

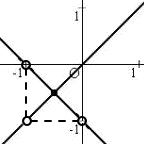
　よって、Ａ ＝ Ｂ （≠−１） または　Ａ＋Ｂ＋１＝０ を満たす−１以外の全てのＡ、Ｂ

　これに対して、上の比例式を、ちょっとだけ一般化したと思われる次の比例式

　　　　　　　

の場合は、少し事情が違ってくる。上の比例式を満たす実数 Ａ、Ｂ、Ｃ は、実は、
　　　　　　　　　　Ａ ＝ Ｂ ＝ Ｃ （≠−１）
という場合しかない。実際に、比例式＝Ｋ　とおいて、分母を払うと、
　　　　　　　Ａ＝Ｋ（１＋Ｃ）
　　　　　　　Ｂ＝Ｋ（１＋Ａ）
　　　　　　　Ｃ＝Ｋ（１＋Ｂ）
　　Ａ＝Ｋ（１＋Ｃ）　と　Ｂ＝Ｋ（１＋Ａ）　を辺々引いて、　Ａ−Ｂ＝Ｋ（Ｃ−Ａ）
　　Ｂ＝Ｋ（１＋Ａ）　と　Ｃ＝Ｋ（１＋Ｂ）　を辺々引いて、　Ｂ−Ｃ＝Ｋ（Ａ−Ｂ）
　　Ｃ＝Ｋ（１＋Ｂ）　と　Ａ＝Ｋ（１＋Ｃ）　を辺々引いて、　Ｃ−Ａ＝Ｋ（Ｂ−Ｃ）
　これらの３式を辺々掛けて、
　　　　　　　　(Ａ−Ｂ)(Ｂ−Ｃ)(Ｃ−Ａ)＝Ｋ³(Ａ−Ｂ)(Ｂ−Ｃ)(Ｃ−Ａ)
よって、Ｋは実数なので、
　　　　　　　　Ａ＝Ｂ　または　Ｂ＝Ｃ　または　Ｃ＝Ａ　または　Ｋ＝１
ここで、Ｋ＝１　とすると、３＝０　となり矛盾。
　　　　　Ａ＝Ｂ　とすると、Ｂ−Ｃ＝Ｋ（Ａ−Ｂ）＝０　より、Ｂ＝Ｃ
　　　　　　　　　よって、　Ａ ＝ Ｂ ＝ Ｃ （≠−１）
　　　　　Ｂ＝Ｃ、Ｃ＝Ａ　のときも同様で、
　　　　　　　　　　　　　　　Ａ ＝ Ｂ ＝ Ｃ （≠−１）
　したがって、比例式を満たす Ａ、Ｂ、Ｃ　は、　Ａ ＝ Ｂ ＝ Ｃ （≠−１）　となる。

　文字の個数が増えると、それだけ制約が厳しくなるのだろう。とても、不思議な現象だ。