角が6つのグラフを描いてみました。: x4y2 + 2x3y3 + x2y4 = 10
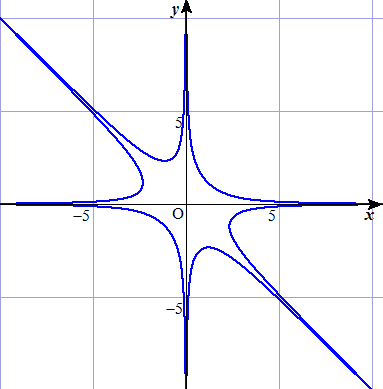
上の係数2を少しでもずらすと形が変わってしまいます。
らすかるさんからのコメントです。(平成26年5月6日付け)
角が6つならば、 x6-6x4y2+9x2y4=10 にするときれいですね。
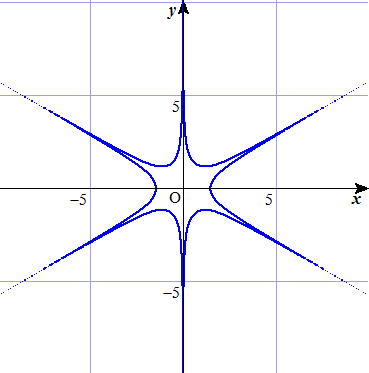
DD++さんからのコメントです。(平成26年5月6日付け)
同じ手法で、x10-20x8y2+110x6y4-100x4y6+25x2y8=10 とすると10個の角ができますね。
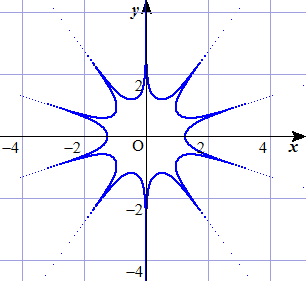
この方法で奇数個のものはうまくできるでしょうか?
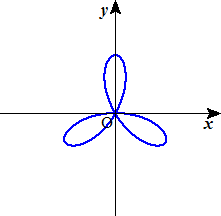
GAI さんからのコメントです。(平成26年5月6日付け)
(x2+y2)2+3x2y-y3=0 (-1<x<1)
らすかるさんからのコメントです。(平成26年5月6日付け)
x6-6x4y2+9x2y4=10 を極方程式に直すと、r={20/(1+cos(6θ))}^(1/6) となり、
x10-20x8y2+110x6y4-100x4y6+25x2y8=10 を極方程式に直すと、
r={20/(1+cos(10θ))}^(1/10)
となりますので、一般に、r={20/(1+cos(nθ))}^(1/n) とすれば角がn個になりますね。
よって、例えば、r={20/(1+cos(5θ))}^(1/5) とすれば角が奇数個になります。
r={20/(1+cos(5θ))}^(1/5) を直交座標の方程式に直すと、
25x8y2-100x6y4+40x5+110x4y6-400x3y2-20x2y8+200xy4+y10 = 400
となりますので、これが角が5個の式です。
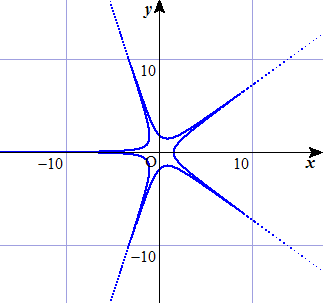
DD++さんからのコメントです。(平成26年5月7日付け)
私が気になっていたのは、この部分の処理で、偶数個の場合は、r2=x2+y2 と rcosθ=x で
そのまま全て処理できるのですが、奇数個の場合は、rが1つ余るため両辺2乗する処理が
必要になります。
ところが、方程式で両辺2乗するというのは、一般には同値変形ではなく、例えば、直線
y=x の両辺を2乗した y2=x2 は2直線になりますし、円 y2=1-x2 は両辺2乗すると、円+双曲
線に、と描く曲線が増えるはずです。
r(x2+y2)2=20-x5+10x3y2-5xy4 は果たして両辺2乗してしまって大丈夫なのでしょうか?
一般の奇数次の場合には?
らすかるさんからのコメントです。(平成26年5月7日付け)
一般の奇数次も含め、両辺2乗して大丈夫です。
r={20/(1+cos(nθ))}^(1/n) から、rn(1+cos(nθ))=20 より、rn=20-rn・cos(nθ)
この式の両辺を2乗すると、rn=20-rn・cos(nθ) または rn=-{20-rn・cos(nθ)} と同値になり
ますが、後者の式は、rn=rn・cos(nθ)-20 という常に(左辺)>(右辺)の式であって、成り立つ
ことがありませんので、2乗しても同値性が崩れません。
DD++さんからのコメントです。(平成26年5月7日付け)
そうか、なるほど、極方程式の状態のまま考えればよかったのですね。すっきりしました。
ありがとうございます。
