・　鮮やかな計算　　　　　　　　　　　　　　　　　　　Ｓ．Ｈ氏

　計算問題で、単なる式の変形で求まる問題はつまらないが、式の背後に図形が絡んでくる
と、話は違ってくる。式そのものに俄然輝きが増してくる。

　３世紀頃の中国（三国時代）に、劉徽という人がいた。彼は漢の時代にまとめられたとされる
数学書「九章算術」を愛読書とし、その注釈書を書き上げている。

　彼は、次のような問題に対して、ユニークな解法を残している。

　問題　縦と横の長さが不明な戸口がある。
　　　　長さがやはり不明な棒を持った人が、この
　　　　戸口を通り抜けようとする。
　　　　　棒を横にすると、戸口より、２ｍ長く、棒を
　　　　縦にすると、戸口より、１ｍ長い。斜めにす
　　　　ると、戸口とピッタリだという。（左図参照）
　　　　　このとき、戸口の縦・横の長さを求めよ。

　　この問題は、中学３年生レベルの問題で、今
　の中学生は次のように解くであろう。

　　棒の長さを、Ｘ ｍ とする。三平方の定理から、
　　　　　　（Ｘ−２）²＋（Ｘ−１）²＝Ｘ²
　　　これを解いて、　Ｘ＝１，５
　　　　　　　　　　　　　　　　　　　　　　　　　　　　Ｘ＝１　とすると、
　　　　　　　　　　　　　　　　　　　　　　　　　　　戸口の縦の長さが、０ｍになってしまうので不適。
　よって、Ｘ＝５　が解となる。このとき、戸口の縦の長さは、４ｍ、横の長さは、３ｍとなる。

　これに対して、劉徽は次のように考えた。

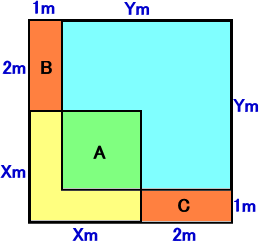　　戸口の横の長さを、Ｘｍ、縦の長さを、Ｙｍとする。
　このとき、三平方の定理から、
　　一辺が棒の長さ（＝Ｘ＋２＝Ｙ＋１）の正方形の面
　積は、
　　　一辺が戸口の横の長さ（＝Ｘ）の正方形の面積
　　と、
　　　一辺が戸口の縦の長さ（＝Ｙ）の正方形の面積
　の和に等しい。
　　このとき、左図において、　　Ａ＝Ｂ＋Ｃ
　となる。
　　よって、Ａ＝（Ｘ−１）²＝２×１＋１×２＝４　から、
　　　　Ｘ−１＝２　すなわち、Ｘ＝３
　同様にして、Ａ＝（Ｙ−２）²＝４　から、Ｙ＝４

　上記計算を一般化すれば、次のようにまとめられる。（九章算術に載っている解法）

（戸口の横の長さ）＝戸口の縦・横のはみ出し分の積の２倍を開平し、
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　戸口の縦のはみ出し分を加える

（戸口の縦の長さ）＝戸口の縦・横のはみ出し分の積の２倍を開平し、
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　戸口の横のはみ出し分を加える

（練習問題）　縦と横の長さが不明な戸口がある。長さがやはり不明な棒を持った人が、この
　　　　　　　　戸口を通り抜けようとする。棒を横にすると、戸口より、１２０ｃｍ長く、棒を縦にす
　　　　　　　　ると、戸口より、６０ｃｍ長い。斜めにすると、戸口とピッタリだという。
　　　　　　　　　このとき、戸口の縦・横の長さを求めよ。

　劉徽の方法を会得された方は簡単でしょう。次のように求められる。

　　　　　　　（戸口の縦の長さ）＝

　　　　　　　（戸口の横の長さ）＝

いかがでしたか？

（参考文献：山下純一　著　数学史物語（東京図書））