２直線の交点を通る直線の計算、２円の交点を通る直線の計算、２球の交円を含む平面の計
算などに対して、次の公式はよく知られている。
２つの図形の方程式 Ｆ(Ｘ，Ｙ)＝０ 、Ｇ(Ｘ，Ｙ)＝０ の交わりを含む図形の方程式は、
ｈ・Ｆ(Ｘ，Ｙ)＋ｋ・Ｇ(Ｘ，Ｙ) ＝ ０ （ただし、ｈ、ｋ は同時に０でない）
と書ける。
２つの図形が交わっていれば、上の公式は意味がある。しかし、問題は、交わっていなくても、
上記の公式を用いると、何がしかの方程式が得られるということである。
(例） ２つの円 Ｘ2＋Ｙ2 ＝ １ 、(Ｘ−１)2＋Ｙ2 ＝ １ は明らかに交わる。２つの方程式を辺々
引いて（ｈ＝１、ｋ＝−１ に相当）、 Ｘ＝１/２ が得られる。これは、２つの円の交点を通る
直線の方程式であり、２つの円の中心を結ぶ線分に垂直である。
(例） ２つの円 Ｘ2＋Ｙ2 ＝ １ 、(Ｘ−４)2＋Ｙ2 ＝ １ は明らかに交わらないが、２つの方程式
を辺々引いて（ｈ＝１、ｋ＝−１ に相当）、 Ｘ＝２ が得られる。これは、２つの円の中心を
結ぶ線分に垂直な直線の方程式である。
この問題に対して、自分なりに次のように理解していた。
２つの図形Ｆ、Ｇに対して、
「点Ｐは、ＦとＧの交点」 ならば、「点Ｐは、図形 ｈ・Ｆ＋ｋ・Ｇ＝０ 上の点」
という命題において、交わりがない場合は、仮定が「偽」なので、上の命題は、無内容的に成り
立つ。したがって、交わりがなくても、方程式 ｈ・Ｆ＋ｋ・Ｇ＝０ は意味を持つ。
私自身の解釈では自信がなかったので、ひろく教えを請うために教科書会社のＨＰに次のよ
うな書き込みなどもした。
『中心の異なる２つの円があるとします。２つの円が交わるとき、２つの円の方程式を辺々引
くと、２つの円の交点を通る直線の方程式が得られます。この直線は、２つの中心を結ぶ直
線に垂直です。２つの円が交わらないとき、形式的に、上記の計算を行うと、やはり、２つの
円の中心を結ぶ直線に垂直な直線の方程式が得られます。私の感覚からすると、交わって
いないので、２つの円の方程式同士を引き算することは出来ないと思うのですが、皆さん、
どうお考えでしょうか？お教えください。交わっていないときは、２つの解集合の交わりが空
集合で、空集合上で計算している感じで馴染めません。よろしくお願いします。』
この書き込みに対して、そのサイト内では、満足のいく反応を得ることができなかった。
この問題に対して、数学セミナー（１９９９年２月号（日本評論社））の中の記事
「交わらない２円の交点を通る直線の存在」（岡部恒治・中村文則）
が、それまでのモヤモヤを一気に解消してくれた。
「交わっていなければ、交わるようにすればよい！」というごく自然な発想が、私を「はっ！」
と、させた。すなわち、２つの円 Ｘ2＋Ｙ2 ＝ １ 、(Ｘ−４)2＋Ｙ2 ＝ １ において、中心を変えず、
右辺の値を、両者とも同じ数だけ少し水増しするのである。即ち、２つの円として、
Ｘ2＋Ｙ2 ＝ ９ 、(Ｘ−４)2＋Ｙ2 ＝ ９
としても、辺々引いた結果は、Ｘ＝２ で一致する。
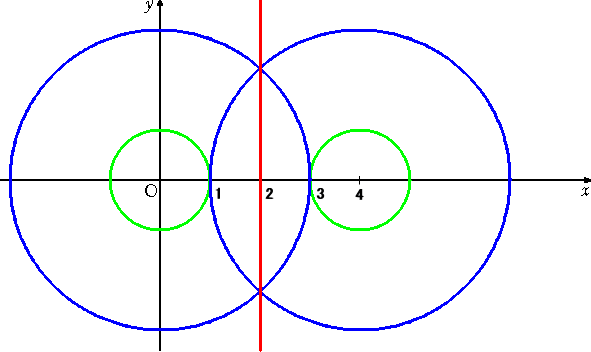
上の図を見ると、交わっていないのに得られてしまうという直線の意味が分かってくる。
ところで、２つの円の交点を結ぶ直線は必ず２つの円の中心を結ぶ線分に垂直であるが、さら
に、次のような驚くべき性質をもつことも教えられた。
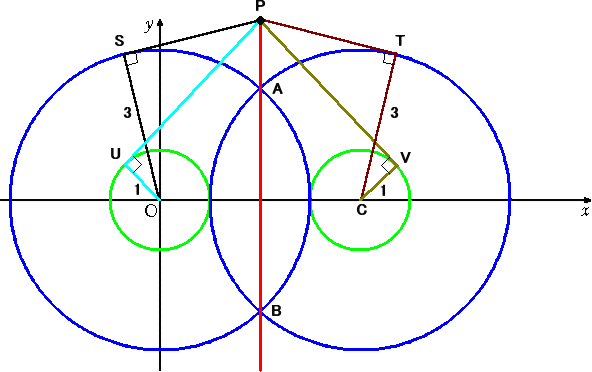
方べきの定理から、ＰＳ2 ＝ ＰＡ・ＰＢ ＝ ＰＴ2 であるので、明らかに、ＰＳ ＝ ＰＴ である。
ところで、ＰＵ2 ＝ ＰＯ2−ＯＵ2 ＝ ＰＳ2＋ＯＳ2−ＯＵ2
ＰＶ2 ＝ ＰＣ2−ＣＶ2 ＝ ＰＴ2＋ＣＴ2−ＣＶ2
において、ＰＳ ＝ ＰＴで、また、ＯＳ2−ＯＵ2 ＝ ＣＴ2−ＣＶ2 ＝（水増し分） であることから、
ＰＵ ＝ ＰＶ が成り立つ。
（この証明は、２つの円の半径が異なる場合も有効であることに注意する。）
したがって、２つの円が交わっている、いないに関わらず、２つの円から得られる直線にお
いて、
直線上の任意の点から、それぞれの円に引いた接線の長さは常に等しい
という性質を持つことが分かった。
この事実は、私のこれまでの認識を変える、非常に驚くべき結果である。
