当HPがいつもお世話になっているS(H)さんが、「およげ!たいやきくん」で有名になった
毎日毎日、僕らは鉄板の〜上で焼かれて嫌になっちゃうよ〜♪
という懐かしい唄(子門真人 1976年)とともに出題している問題に興味を持った。
九州大学の問題とのことである。(→ 参考)
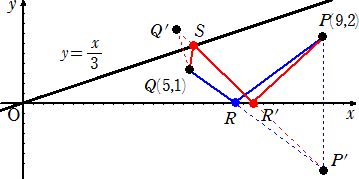
座標平面上に直線 L:y=(1/3)x と点P(9,2)、Q(5,1)がある。以下の問いに答えよ。
(1) 座標平面上の点をx軸に関して対称な点に移す移動(1次変換)を表す行列Aを求めよ。
(2) 座標平面上の点を直線L関して対称な点に移す移動(1次変換)を表す行列Bを求めよ。
(3) 点Rをx軸上を動く点とする。このとき、折れ線PRQの長さの最小値を求めよ。
(4) 点Rをx軸上を動く点、点Sを直線L上を動く点とする。このとき、折れ線PRSQの長さの
最小値を求めよ。
「毎日毎日、僕らは鏡みて〜数学学んで好きになっちゃうよ〜」と、鏡を二枚使えば解けてし
まう問題とのことで、次のように解いてみた。
(解) (1) A=[[1,0],[0,-1]] (2) B=[[4,3],[3,-4]]/5
(3) 鏡映変換により、 P’(9,−2)なので、
折れ線PRQの長さの最小値=線分P’Qの長さ=5
(4) 鏡映変換により、 Q’(23/5,11/5)なので、
折れ線PRSQの長さの最小値=線分P’Q’の長さ=√(37) (終)
(コメント) S(H)さんは極値問題に持って行きたい意向のようだが、受験数学では、上記の
問題は鏡映変換で解くのが定石でしょう。
