富士見市、富士見町、富士見村、富士見坂、富士見台など、日本各地に「富士見」と名の
付く地名は多い。富士山が見えるから「富士見」とついているわけであるが、一体どこら辺ま
で富士山を見ることができるのだろうか？
ものの本によると、埼玉県南東部にある富士見市は富士山から９０ｋｍほど離れているが、
障害物がなければ十分富士山が見えるという。
地球を半径約６３７８ｋｍの球体と考え、３７７６ｍの富士山頂からどこまで見えるか計算し
てみよう。
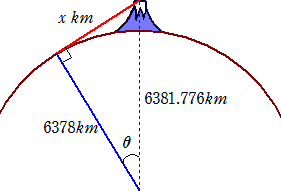左図において、ｃｏｓθ＝6378/6378.3776=0．999408315177468
このとき、θ≒0．0344018365855183（ラジアン）
（度数法では、1．97108004384895°）
より、ｘ＝6378ｔａｎθ≒219．501512924145
ということは、富士山山頂から２１９ｋｍ離れた
所から、もしかしたら富士山が見えるかも．．．。
因みに、
茨城県東海村が２０７ｋｍ、栃木県那須塩原市が２１４ｋｍ、三重県津市が２１４ｋｍ、
三重県志摩市が２０９ｋｍ、・・・。
富士山が見える地域は、関東平野の大半、関東・中部地方の山々と言われるが、条件さ
え整えば、近畿地方東部の山や志摩半島の海岸からも見えるらしい。さすが！日本最高峰
の山だ。そのことを知ると不思議なことがある。富士山が見えない地域なのに、「富士見町」
と名の付く地名もある。例えば、山形県酒田市富士見町など。これは「出羽富士」と言われる
鳥海山が見えることから命名されたらしい。
私の大好きな羊蹄山（１８９８ｍ）は「蝦夷富士」とも言われるので、北海道にも「富士見」と
名のつく地名はあるのかな？探したら、ありました！
北海道茅部郡森町富士見町 、北海道二海郡八雲町富士見町
何れも渡島総合振興局管内の自治体で、羊蹄山の対岸にある。きっと綺麗に見えるんで
しょうね。
（追記） 平成２６年９月２３日付け
９月２３日付けの朝日新聞朝刊に上記に関連する話題が掲載されていた。
富士山が見える西側の限界とされる滋賀県白倉岳の南側の尾根（標高９１５ｍ 京都市左
京区）から富士山頂の撮影に、奈良県天理市の住職 新林正真さんが成功した。富士山頂ま
での距離は約２６１ｋｍで、微かに富士山剣が峰が木の隙間からピンポイントで見えたという。
現在、富士山の撮影は２０都府県で確認されている。
北は、福島県の日山（富士山より、２９９ｋｍ）、東は千葉県犬吠埼（富士山より、１９８ｋｍ）、
南東は八丈島の三原山（富士山より、２７１ｋｍ）で、最も遠いのは南西の和歌山県色川富士
見峠（富士山より、３２２．９ｋｍ）という。
（追記） 令和３年６月１９日付け
自宅から５分も歩くと海に出る。サーフィンに興じる若者が多い。遠くに水平線が見える。
ふと、今見ている水平線は何ｋｍ先にあるのだろうかと疑問が湧いた。
地球は球体と仮定し、その半径Ｒは、Ｒ＝６３７８ｋｍとする。身長ｈをｈ＝１．８ｍとすると、
次式が成り立つ。
水平線までの距離をｄとして、 ｄ2＝（Ｒ＋ｈ）2−Ｒ2＝２Ｒｈ＋ｈ2＝２Ｒｈ（１＋ｈ/（２Ｒ））
１＋ｈ/（２Ｒ）＝１＋１．８/１２７５６０００＝１．００００００４１ なので、これはほとんど１と考
えてよいだろう。
よって、 ｄ＝√（２Ｒｈ）＝√（１２７５６０００×１．８）＝４７９１．７４２８９７
以上から、海岸では、４〜５ｋｍ先を見ていることになるんですね！意外と近いかも．．．。
東京スカイツリー（ｈ＝６３４ｍ）から水平線を見ると、同様の計算をして、
８９９２９．４３９ｍ となるので、約９０ｋｍ先となります。これは、南は熱海あたりまで、東は
銚子あたりまでとなります。
ＧＡＩ さんからのコメントです。（令和４年５月８日付け）
NHKの人気番組の「チコちゃんに叱られる」を見ていたら、一度西に沈んだ太陽を再び見
るために、垂直に立つ塔へある距離をある時間内に登ると、再びその太陽の姿を望めると
いう話題が取り上げられていた。
そして、それを可能とする公式が当時中学３年生であった工藤優輝(ゆうよう)君が見つけ
て、科学論文コンクールで最優秀賞を受けたとあり、その式が
H(t)=10^3*(sqrt((6400*cos(θ)*tan(t/240))^2+(6400*cos(θ))^2)-6400*cos(θ)) (m)
と紹介されていた。(θは地球上での緯度(度)、tは上に登るのに時間(秒)
東京スカイツリーがある場所の緯度が北緯３６度で、地球の半径を６４００(km)の真球とし
ている。
計算機での計算上、角度の単位をラジアンへ変更して、
H(t)=10^3*(sqrt((6400*cos(36*Pi/180)*tan(t/240*Pi/180))^2+(6400*cos(36*Pi/180))^2)
-6400*cos(36*Pi/180)) (m)
ｔ を１０（秒)刻みで算出してみると、
t ;H(t)(m)
10;1.369115132
20;5.476464147
30;12.32205791
40;21.90591451
50;34.22805931
60;49.28852487
70;67.08735103
80;87.62458486
90;110.9002806
100;136.9145000
110;165.6673116
120;197.1587915
130;231.3890231
140;268.3580969
150;308.0661105
160;350.5131691
170;395.6993849
180;443.6248773
････････････
従って、第一展望台がある（高さ350m)までは１６０秒かけて登れば、沈んだ太陽は再び目
にすることが可能で、実際、スカイツリーのエレベータではここまでの到達時間が５０秒なの
で、太陽が西に沈んで直ぐにエレベータで展望台に登れば、残り１１０秒間は再び太陽の姿
を見ることが出来ることになる。
上記の数値の並びが徐々に開いていくので、１０秒間隔の開きを四捨五入で m 単位の整
数で並べてみると、
1, 4, 7, 10, 12, 15, 18, 21, 23, 26, 29, 31, 34, 37, 40, 42, 45, 48, 51, 53, 56, 59, 62,64, 67, 70, 73,･･･
となっていった。これを、OEISで試したら「A186226」に70までの数列に合致した。
(73は72でそこでずれる)
この数列は、triangular numbers (三角数)とpentagonal numbers (五角数)に深く関連した
ものになっており、あくまでも偶然ではあろうが、天体の運行が幾何学的構造で動かされて
いるのではないかと思ってしまうほど重なることに驚いた。
