平成26年度大学入試センター試験 数学I・Aで街路図の問題が久々に(1986年本試験、
1995年追試以来?)出題された。新学習指導要領では期待値が数学Aから外れたことを
意識しているのか、問うてもいいはずの期待値の問題がなかったのが意外か?
ちょっと面白そうに見えたので解いてみた。下の図はある町の街路図の一部である。
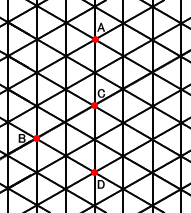
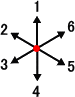
ある人が、交差点Aから出発し、次の規則に従って、交差点から隣の交差点への移動を
繰り返す。
(イ) 街路上のみを移動する。
(ロ) 出発前にサイコロを投げ、出た目に応じて上図の1-6の矢印の方向の隣の交差
点に移動する。
(ハ) 交差点に達したら、再びサイコロを投げ、出た目に応じて図の1-6の矢印の方向
の隣の交差点に移動する。(一度通った道を引き返すこともできる。)
(ニ) 交差点に達するたびに、(ハ)と同じことを繰り返す。
(1) 交差点Aを出発し、4回移動して交差点Bにいる移動の仕方について考える。この場合、
3の矢印の方向の移動と4の矢印の方向の移動をそれぞれ2回ずつ行うので、このよう
な移動の仕方は( a )通りある。
(2) 交差点Aを出発し、3回移動して交差点Cにいる移動の仕方は( b )通りある。
(3) 交差点Aを出発し、6回移動することを考える。このとき、交差点Aを出発し、3回の移動
が終わった時点で交差点Cにいて、次に3回移動して交差点Dにいる移動の仕方は( c )
通りあり、その確率は( d )である。
(4) 交差点Aを出発し、6回移動して交差点Dにいる移動の仕方について考える。
・1の矢印の向きの移動を含むものは( e )通りある。
・2の矢印の向きの移動を含むものは( f )通りある。
・6の矢印の向きの移動を含むものも( f )通りある。
・上記3つ以外の場合、4の矢印の向きの移動は( g )回だけに決まるので、移動の仕
方は( h )通りある。
よって、交差点Aを出発し、6回移動して交差点Dにいる移動の仕方は( i )通りある。
(解) (1) 4C2=6(通り)
(2) Aを出発して、3回移動して交差点Cにいる移動の仕方は、
345、354、435、453、534、543 の6通り
(3) (2)より、6×6=36(通り)
起こりえるすべての場合の数は、 66=46656(通り)
よって、求める確率は、 36/46656=1/1296
(4) ・1の矢印の向きの移動を含むものは、
144444、414444、441444、444144、444414、444441 の6通りある。
・2の矢印の向きの移動を含むものは、 2、5、4、4、4、4 の順列の数に等しいから、
6!/4!=30(通り)ある。
・6の矢印の向きの移動を含むものも、上と同様に、30通りある。
・上記3つ以外の場合、4の矢印の向きの移動は、2回だけに決まるので、移動の仕方
は、 3、3、4、4、5、5 の順列の数に等しいから、6!/(2!2!2!)=90(通り)
よって、交差点Aを出発し、6回移動して交差点Dにいる移動の仕方は、156通りある。
(コメント) 問題を見て一瞬面白さを感じたが、実際に解いてみると、それほどインパクトの
ある問題ではなかった。受験生にとっては取り組みやすい問題だったろう。
