平成２５年１１月２３日に筑波大付属駒場高校で研究大会があり、中学１年生の授業を見
学する機会があった。
「数学を自由に考え、楽しむ」という授業の方針のもと、楽しんだ先に、その中から何かを
発見していくという流れで、生徒たちが自ら数学の教育目標を体現していく様を見て非常に
感動した。
５０分という授業の中で与えられた課題は次のようなものであった。
階段状のマス目に数字をルールに従って書き込み、縦に足して「９９９９・・・」を作る。
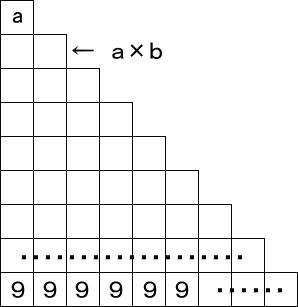（１） まず、最上段に数字「ａ」を書き込む。（２） その数字をｂ倍したものを次の段に右
詰で書き込む。
（３） （２）で得られた値をさらにｂ倍し、次の
段に右詰で書き込む。
（４） 以下、この手順を繰り返す。
（５） 縦に足してみる。
（６） 「９９９９９９・・・」は作れているか？
上記のような手順で得られる表を、
（ａ，ｂ）と書くことにする。
（ａ，ｂ）がどのような場合に、「９９９９９９・・・」は作れるのだろうか？
生徒たちは、（９，１）で「９９９９９９・・・」が作れることを直ぐ見いだし、（８，２）の作業を始
めた。（８，２）は次のようになる。
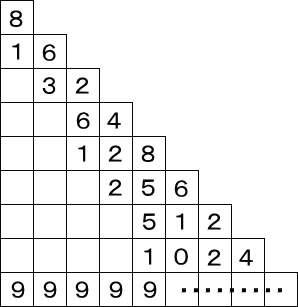（９，１）が、９＋１＝１０で、（８，２）も８＋２＝１０ ということから、ａ＋ｂ＝１０ で
ある（ａ，ｂ）では、「９９９９９９・・・」が作れる
のではないかという声が出始め、実際に、
（７，３）に挑戦し成功するものも現れた。
授業はまさに活況を呈し、生徒たちの知的
好奇心が最高潮に達しているようだった。
授業担当者の「なぜ、そうなるのだろう？」
という問いかけに敏感に反応した生徒が何
人かいた。
その中の一人が「驚くべき着想」で、答を
導いた。
（解） （ａ，ｂ）の表で、段が下がる度に数が右にずれていくので、１列目と２列目の間に小
数点があるように数をとらえ直す。（← 驚くべき着想！）
１段目＝ａ
２段目＝ａ×ｂ/１０ （← 「/１０」という発想は本当に素晴らしいですね！）
３段目＝ａ×（ｂ/１０）2
４段目＝ａ×（ｂ/１０）3
５段目＝ａ×（ｂ/１０）4
・・・・・・・・・・・・・・・
（会場からは、「エッ！、中学１年生が無限等比級数を使うの？というどよめきがあった。）
生徒は、５段目までを加えて、
ａ＋ａ×ｂ/１０＋ａ×（ｂ/１０）2＋ａ×（ｂ/１０）3＋ａ×（ｂ/１０）4
＝ａ（１＋ｂ/１０＋（ｂ/１０）2＋（ｂ/１０）3＋（ｂ/１０）4）
ここで、 ａ＋ｂ＝１０の場合を考えると、 ａ＝１０−ｂ なので、
上式＝（１０−ｂ）（１＋ｂ/１０＋（ｂ/１０）2＋（ｂ/１０）3＋（ｂ/１０）4）
＝（１０＋ｂ＋ｂ2/１０＋ｂ3/１０2＋ｂ4/１０3）−（ｂ＋ｂ2/１０＋ｂ3/１０2＋ｂ4/１０3＋ｂ4/１０4）
＝１０−ｂ5/１０4
「ｂ5/１０4」は、「０．０００・・・」という数なので、この式より、「９．９９９９９・・・」が作れること
が理解される。 （終）
無限等比級数という言葉を知らなくても、無限等比級数的に物事をとらえ、そして、無限等
比級数的に数式処理しているという驚くべき解答を、中学１年生がわずか５０分の時間の中
で到達したことに会場に居合わせた方は皆、驚いていた。
生徒たちは、ａ＋ｂ＝９、８、７、・・・ の場合を考え始め、その一般化に到達した生徒もい
た。そこにはもう生徒たちの知的探求心を止める術はないようだった。
このように、生徒の発想を大切にする教育がなされている所がまだ日本にあることに素直
に感動し、日本の数学の未来は安泰だと実感した、そんな充実した一日だった。
