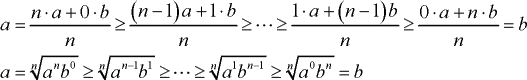(相加平均と相乗平均の不等式)
の更なる一般化
(マクローリンの不等式)
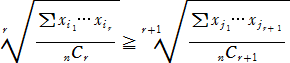
上記の不等式において、r=1としたときの左辺が相加平均で、r=n−1としたときの右
辺が相乗平均である。
n個の数について、相加平均をAn、相乗平均をGnとおくと、
ヤコブスタール(Jacobsthal)の不等式
n(An−Gn)≧(n−1)(An-1−Gn-1)≧・・・≧2(A2−G2)≧0 (n≧2)
のように、不等式の連なった列について、他にどのようなものがあるでしょう。
ヤコブスタール(Jacobsthal)の不等式から(相加平均と相乗平均の不等式)を示すことは
できるが、逆は成り立たない。
DD++さんからのコメントです。(平成29年2月16日付け)
上記についてですが、そうでもないようです。
n個の数の総和を考えると、 nA[n] = (n-1)A[n-1] + x[n]
n-1個の G[n-1] と1個の x[n] に相加平均と相乗平均の大小関係を用いると、
G[n] ≦ { (n-1)G[n-1] + x[n] } /n
第2式を -n 倍して辺々足し合わせれば、ヤコブスタールの不等式の左端が得られます。
そこから先も全く同様の証明を繰り返すだけです。
(追記) 平成25年11月9日付け
(an+bn)/2≧{(a+b)/2}n はよく見られますが、より強い意味で、
が成り立つので、次の不等式の列が成り立ちます。
さらに、
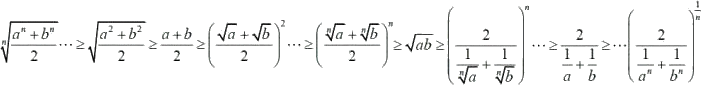
が成り立ちます。
(追記) 平成25年12月9日付け
項数が3個以上のときも、同様の不等式の列が存在する。
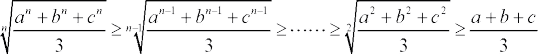
そのため、一般に以下のことが成り立つことを示す。
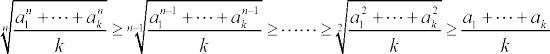
(追記) 平成26年1月17日付け
条件付きで、 a≧b のとき、