・ベン図の限界 S.H氏
集合の要素の個数を計算する問題では、ベン図が有効に使われる。
次の問題は、近畿大学(1999)の問題であるが、東京大学(1965)の集合論先駆けの
有名問題に類似している。
例 生徒数50人のあるクラスで、A、B、Cの3種類の本を読んだかどうかを調査したところ、
次の結果を得た。
(a) Aを読んだ生徒は35人
(b) Bを読んだ生徒は23人
(c) Cだけを読んだ生徒は2人
(d) B,Cの両方を読んだ生徒は11人
(e) A,Cの少なくとも一方を読んだ生徒は44人
(f) B,Cの少なくとも一方を読んだ生徒は25人
(g) A,B,Cのうちどれか1種類だけを読んだ生徒は31人
(1) クラスの生徒数に対して、Aを読んだ生徒の割合は( )%であり、Bを読んだ生徒の
割合は( )%である。また、(b)(d)(f)から、Cを読んだ生徒は( )人であり、その
割合は( )%である。
(2) A,Cの両方を読んだ生徒は( )人であり、A,Bの両方を読んだ生徒は( )人であ
る。
(3) Aだけを読んだ生徒は( )人である。また、Bだけを読んだ生徒は( )人である。
(4) A,B,Cをすべて読んだ生徒は( )人である。A,B,Cのどれも読まなかった生徒は
( )人である。
(5) A,Bの少なくとも一方を読んだ生徒は( )人である。
ベン図から平面が、23=8個の区画に分かれるので、各区画に a、b、c、d、e、f、g、h
と未知数をおいて、連立方程式を立てれば容易に解かれることだろう。
私自身、このような問題に対しては、円を3つ書いて条件を当てはめて解いてきたが、A、
B、C、D、・・・と集合が4つ以上ある場合に、どのように円を描くのか、一瞬途方に暮れてし
まう。(もっとも、集合が4つ以上あるときの個数定理を使う問題は私自身まだ見たことがないが...。)
また、ベン図は、細かい条件を記入するときに書きにくいという弱点を常々感じていた。
このような場合、次のような表形式にすると、集合が何個あっても問題は起こらないという
ことを、
長岡亮介 著 「東大の数学入試問題を楽しむ」 (日本評論社)
で最近学ぶことができた。
| |
A |
B |
C |
|
人数 |
| イ |
○ |
○ |
○ |
|
a |
| ロ |
○ |
○ |
× |
|
b |
| ハ |
○ |
× |
○ |
|
c |
| ニ |
× |
○ |
○ |
|
d |
| ホ |
○ |
× |
× |
|
e |
| ヘ |
× |
○ |
× |
|
f |
| ト |
× |
× |
○ |
|
g |
| チ |
× |
× |
× |
|
h |
|
条件より、 a+b+c+e=35 、 a+b+d+f=23 、g=2
a+d=11 、a+b+c+d+e+g=44
a+b+c+d+f+g=25 、e+f+g=31
が成り立つ。このとき、 g=2 より、
a+b+c+e=35 、 a+b+d+f=23 、a+d=11 、
a+b+c+d+e=42 、a+b+c+d+f=23 、e+f=29 |
よって、 c=23−23=0 、d=42−35=7 で、 a=11−7=4
式を整理して、 b+e=31 、b+f=12 より、 e−f=19
よって、 e=(29+19)/2=24 、f=(29−19)/2=5 より、 b=7
h=50−(4+7+0+7+24+5+2)=50−49=1
| したがって、 |
| |
A |
B |
C |
|
人数 |
| イ |
○ |
○ |
○ |
|
4 |
| ロ |
○ |
○ |
× |
|
7 |
| ハ |
○ |
× |
○ |
|
0 |
| ニ |
× |
○ |
○ |
|
7 |
| ホ |
○ |
× |
× |
|
24 |
| ヘ |
× |
○ |
× |
|
5 |
| ト |
× |
× |
○ |
|
2 |
| チ |
× |
× |
× |
|
1 |
|
表より、
(1) A:35/50*100=70%
B:23/50*100=46%
C:4+0+7+2=13人
13/50*100=26%
(2) A、C:4+0=4人
A、B:4+7=11人
(3) A:24人 B:5人
(4) A、B、C:4人 、1人
(5) 4+7+0+7+24+5
=47人 |
基本的に、連立方程式を解くことに変わりはないが、作図段階で苦労することなく立式が
出来る点で、これはまさにベン図の限界からの解放といっても言い過ぎではないだろう。
(追記) 平成29年3月12日付け
集合論において、ベン図は状況の理解に活躍する。基本的な問題は

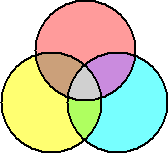
などのベン図を描くことにより、視覚的に解くことができる。
ここで非常に残念な結果が知られている。
4つの円では、ベン図を作ることはできない
そんなわけで、長岡亮介先生の手法に流れるか、包除原理のお世話になるかのどちらか
なのだろう。
でも、これでめげてはいけない。
4つの円ではベン図は作れないが、4つの長方形ではベン図は作れる
ことが知られている。例えば、次のように考えればよい。
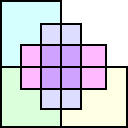
また、4つの楕円でもベン図を作ることができる。
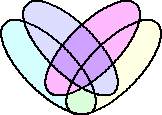
(追記) 平成29年3月19日付け
S(H)さんより、「4つの円では、ベン図を作ることはできない」の証明が掲載されている
HPサイト「Are Venn Diagrams Limited to Three or Fewer Sets?」をご紹介いただきました。





