双曲線関数
ことは易しい。
・ 面積計算の苦労 S.H氏
双曲線関数 ことは易しい。 |
において、直線 X=1、X=2、X軸で囲まれた部分の面積を計算する |
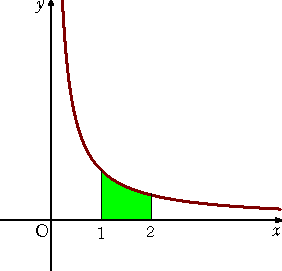 それは、ニュートン、ライプニッツによる微分
それは、ニュートン、ライプニッツによる微分
積分学の確立によっている。かれらは、微分
と積分の関係を明らかにし、図形の面積計算
に画期的な進歩をもたらした。
実際に、面積を計算すれば、
![]()
である。(おおよそ、0.6931471806・・・)
しかしながら、微分積分学が誕生して初めて
左図のような図形の面積が求められたわけで
はないことを、我々はしっかり心に留めて置か
なければならない。
そこには人類の飽くなき挑戦の歴史がある。
微分積分学の発見以前、ブラウンカー(1620〜1684)は、上図の面積を次のように計算した。
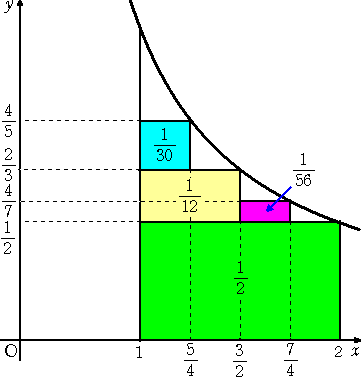
上図のように区間 [1,2] で2分割を繰り返して、小さい長方形を積み上げていく。
このとき、求める面積Sは、
![]()
すなわち、
![]()
各項に部分分数分解を施せば、
![]()
となる。
後は、地道に、この分数計算を実行すればよい。
私自身、すぐ値が 0.69314・・・に近づくだろうと思って、関数電卓を使用して、50項まで計
算してみたが、いっこうに埒があかず、止めてしまった。この級数は涙が出るくらい収束するスピ
ードが遅い。でも、多分昔の人は、そんなことにめげずに、ひたすら計算したに違いない。頭が
下がる思いである。
そこで、表計算ソフトの Excel のマクロを活用して求めることにした。使用したマクロは次の
ようである。
Function S(n)
If n=1 Then
S=1
Else
S=S(n-1) + ((−1) ^ (n−1)) * (1/n)
End If
End Function
Excel を起動し、[ツール]−[マクロ]−[Visual Basic Editor] とクリックして Editor
を起動し、[挿入]−[標準モジュール] を選択して、上記を記述すればよい。後は、Excel の
任意のセルに、例えば、 =S(10) と打ち込むと、瞬時に、10項分の計算結果が得られる。
以下に、その計算結果をあげる。
| n | S | n | S | n | S | ||
| 100 | 0.68817 | 1100 | 0.69269 | 2100 | 0.69291 | ||
| 200 | 0.69065 | 1200 | 0.69273 | 2200 | 0.69292 | ||
| 300 | 0.69148 | 1300 | 0.69276 | 2300 | 0.69293 | ||
| 400 | 0.69190 | 1400 | 0.69279 | 2400 | ? | ||
| 500 | 0.69215 | 1500 | 0.69281 | 2500 | ? | ||
| 600 | 0.69232 | 1600 | 0.69284 | 2600 | ? | ||
| 700 | 0.69243 | 1700 | 0.69285 | 2700 | ? | ||
| 800 | 0.69292 | 1800 | 0.69287 | 2800 | ? | ||
| 900 | 0.69259 | 1900 | 0.69288 | 2900 | ? | ||
| 1000 | 0.69265 | 2000 | 0.69290 | 3000 | ? |
上記の表からも分かるように、2300項分計算しても、小数第3位すら正しい値を得ることが
できない。しかし、大体 0.69・・・位ということは確かめられる。
このことからも、積分計算の有り難味が分かるというものであろう。
(参考文献:遠山 啓 著 数学入門(下) (岩波新書))
