最近、平成25年6月18日付けの新聞で、「入試の数学、難し過ぎ? 埼玉、公立高の問
題で論争」という記事を読んだ。
新聞によると、公立高校入試の数学問題が難し過ぎるのではないかと17日の埼玉県議
会一般質問で取り上げられたそうで、点数だけ見れば数学の平均点は42・4点で確かに、
全教科の平均(55・1点)を下回り低い。しかも、正答率0・4%という問題もあったとのこと
で、受験生が手も足も出ない問題は公立高入試としてふさわしいのか」と問われたとのこと
である。
学習指導要領に則って作問されているはずなので、作問が悪いとは一概に言えない。作
問者の要求レベルに対して、受験生の解答能力が追いついていないというのが真実だろう。
どんな問題か興味があって閲覧したところ、難しい問題も散見されるが、問題レベルとして
は標準的かやや易のレベルの問題群と言えるだろう。
作問者の意図するところと解答者の力量。ちょうどいい難易度の落としどころは難しい。
埼玉県高校入試問題(2013) 数学の問題で、少し食指が動いた問題を紹介してみよう。
1(8) ある数nを40で割り、商の小数第2位を四捨五入したら2.0になりました。こ
のような数nのうちで最も小さい数を求めなさい。
(解) 1.95≦n/40<2.05 より、 78≦n<82 題意より、 n=78 (終)
2(1) 下の図のように、円Oの外の点Pから中心Oを通る直線を引き、円との交点を
点Pに近い方からそれぞれ点A、Bとします。また、点Pから円Oに接線を1本引
き、その接点を点Cとします。さらに、点Bからこの接線に垂線を引き、円との交
点をD、接線との交点をEとします。∠APC=32°のとき、∠DCEの大きさxを
求めなさい。
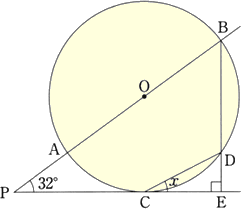
(解) ABは円の直径なので、∠ADB=90°より、ADとPEは平行である。
OCとPEは垂直なので、∠POC=∠AOC=58°
このとき、 ∠ADC=(1/2)∠AOC=29°(← 円周角は中心角の半分)
よって、 x=∠ADC=29°(← 平行線の錯角は等しい) (終)
(コメント) 高校で学習する接弦定理を用いる解法もあるが、手順が煩わしい。上記の解法
が多分一番スッキリする解き方だろう。
