次のような面白い問題に最近出会った。
「立方体の各面に接し、体積がもとの立方体の半分であるような立体を作れ。」
この課題を通して、構図など、デザインの基礎を習熟させるのが目的であると、この課題を出さ
れた方は仰っていた。この問題は、数学的にも興味を引く問題である。
ただ漠然と考えていては何も進まないので、立方体の持つ性質を追究してみよう。
立方体を8個の合同な立方体に分割し、そのうちの4個を用いれば、体積は明らかに半分なの
で、後は、左図のように配置すればよい。
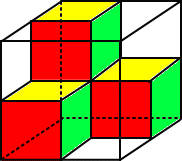
上の立体は、あまりに単純すぎて、造形的な美しさが感じられない。表に出ている3つの立
方体の角を切り取って図形を下図のように配置すれば、多少美しさが感じられる。
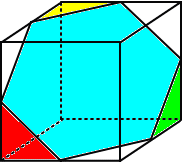
切り取った跡の6個の面が全て同一平面上にあることは、数学的に明らかである。
実際に、もとの立方体の1辺の長さを 2 とし、各辺を座標軸にとれば、上図の緑色の平面の
方程式は、X+Y+Z=3 で与えられる。
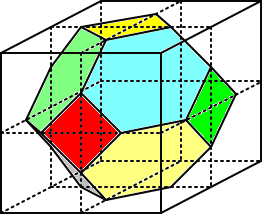
さらに対称性を持たせるために、上図の立体を8個組み合わせたものが、次の立体である。
14個の面が、6個の正方形と8個の正六角形で構成されており、その体積は、この立体に接
する立方体の半分になっている。
もはや、このような立体を見せられて、「体積が半分だよ!」といわれても、一般の人には直
ぐには了解されないだろう。しかし、構成法が分かっている人にとって、この事実は当たり前の
事実である。
上記のような構成法において大切なポイントは、各面の中心をしっかり把握することである。
実際、最初からこのような立体を思い描くことは難しく、中心を結ぶ線により8個の小立方体
に分割し考えたほうが分かりやすい。このような方針のもとに最初の立体は構成されている。
この課題を出された方も、この点を強調されていた。さらに、このような考え方は、遠近法の
作図にも応用されるという。
いま、ある直線上で、等間隔に一定な長さの棒が4本並んでいる。数学的には、このような
配置は次のように示される。

このような作図は、数学の世界では当たり前だが、美術の世界では違和感を感じる。
物を見る場合、自分にとって遠い、近いがあり、物理的に同じ長さでも、視覚的には長さに違い
が生じる。この場合の作図法が、遠近法である。次のように作図すればよいと伺った。

従って、上記の条件を満たす4本の直線を、視覚的に正しく書けば、次のようになる。

しかしながら、数学の世界は目で見える世界そのものを扱う世界ではなく、その物がもつ本
質、イデアの世界を扱うものなので、上記のように単純に4本の直線を書いても、全く違和感
を感じない。この点が、もしかしたら一般の人に数学が受け入れられない原因があるのかも
しれない。
