・　私の未解決問題　　　　　　　　　　　　　　　　Ｋ．Ｓ氏

　「 Ｙ＝｜Ｘ｜^ｘ のグラフをかき、Ｙ＝/２ との交点の個数を求めよ。また、そのときの交
　点のＸ座標を求めよ。」
　これは、自分の考えた問題である。なぜ、こんな問題を思いついたかというと、「０の０乗と
は何か？」という思いがあり、「Ｘ→０ のときの｜Ｘ｜^ｘの極限値は何か？」という問題にた
どり着いたからである。この極限値は対数をとって、ロピタルの定理を使うと １ になる。

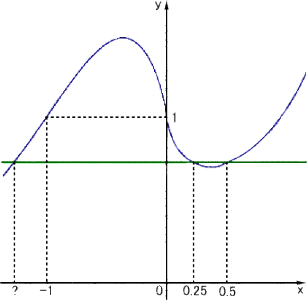そこで、グラフを用いて、 　　　方程式｜Ｘ｜ｘ＝/２ を考えてみる。 　　　グラフから、この解は３個ある。 　　　１/２ と １/４ と負の数の解である。 　　　負の数の解があるということは確かに 　　　分かるのだが、その値は求められなか 　　　った。というわけで、この問題は未だに 　　　解けていない。解がはっきりとした数で 　　　表せないというのは、なんともいえない 　　　気がする。今までに見てきた「数学の 　　　問題」というのには、必ずはっきりした 　　　解があったのに・・・。何とも奇妙である。 　　　こういうわけで深く感銘を受けた。

（追記）　空舟さんからのコメントです。（平成２４年８月２５日付け）

　負の解の問題は、ｔ＝−Ｘ と変換すれば、ｔ^ｔ＝　という問題になりますが、「ランベルトの
W関数」というのがあるらしいです。特殊関数ってやつですね......。


（コメント）　ランベルトのＷ関数を用いて解いてみた。

　ｔ^ｔ＝　の両辺の ｅ を底とする自然対数をとると、　ｔ・ｌｏｇ ｔ ＝ｌｏｇ

　このとき、　ｌｏｇ ｔ ・ｅ^{ｌｏｇ ｔ} ＝ｌｏｇ　なので、　ｌｏｇ ｔ ＝Ｗ（ｌｏｇ）

　よって、　ｔ ＝ ｅ^{Ｗ（ｌｏｇ）}　となる。

　この値を調べるには、数値計算しかなさそうですね．．．。


　らすかるさんからのコメントです。（平成２４年８月２５日付け）

　ランベルトのW関数に関しては以前数値計算方法を研究したことがあって、自作電卓にも
搭載しています。

　ネットで検索すると3次収束と4次収束の式は出てきますが、多桁計算にはちょっと遅いの
で、自作電卓では12次収束の式を使用しています。※漸化式は自作で、24次収束まで作り
ました。

　ところで、　|ｘ|^ｘ=/2 の負の解は、

-log2/{2W(log2/2)}=-1.30435117890103653364720123148623407503553382998902…

となります。

（コメント）　らすかるさん、ありがとうございます。約−１．３位ですか。上図の−１の左側の
　　　　　　部分の視界が少し開けた感じです．．．。


　ＧＡＩさんからのコメントです。（平成２４年８月２５日付け）

　空舟さんから紹介された記事を読んで計算してみました。まず、

　　W(ｘ)=Σ_n=1〜∞ ｛(-n)^n-1/n!｝ｘ^ｎ

で定義される関数Wを作る。（計算機で処理する時には∞を1000で設定しました。）

　ｘ^ｘ=　を満たすｘは、
（一般に、ｘ・e^ｘ=t を満たすｘを求めることがW関数を使うことで出来るようになる。）

　ｘ=log()/W(log() から求まり、

　ｘ=0.3465739502.../W(0.3465739502...)=1.30435117890....

なる値が出る。これから、|ｘ|^ｘ=/2 を満たすｘは、ｘ=1/2、1/4、-1.30435117890....　と３個
存在する。

　ここで、t=-1.30435117890....　に対して、|t|^t=0.7071067811865475244008443619...

一方　/2=0.7071067811865475244008443621...　である。

　同様にして、ｙ=２^ｘ　…　（１）　、ｙ=３ｘ　…　（２）　の２つの交点のｘ座標を求める計算をラ
ンベルトの関数Ｗを用いるやり方で挑戦。

　２^t=3t　から、両辺を ２^t で割って、　1=3te^-t・log2　さらに、両辺を３で割って、

　　1/3=te^-t・log2　　この両辺に -log2 を掛けて、　-(log2)/3=-(log2)te^-t・log2

　これをランベルトの関数を用いて書き換えると、　-(log2)t=W(-(log2)/3)

　これから、　t=W(-(log2)/3)/(-log2)

　これをプログラムに組み、数値計算させると、

　　　t= 0.4578223732320550555738866680640554097777750832317766…

が求まる。これでいいのかな？もう一つの解はどうしたらいいのかな？


　らすかるさんからのコメントです。（平成２４年８月２５日付け）

　W(ｘ)は、-1/e≦ｘ＜0 のとき２価ですから、W(-(log2)/3)は、

-0.317338287203061937813337422441155649112826474209541704773596…

と

-2.296520253118852045622163925693816744412216672265184546034003…

の２つの値をとります。従って、t の値は、

0.457822373232055055573886668064055409777775083231776637656055…

と

3.313178380475634845996561019588783663458454297890271137009552…

の2つです。


　ＧＡＩさんからのコメントです。（平成２４年８月２５日付け）

　W(ｘ)は、-1/e≦ｘ＜0 のとき２価ですから、W(-(log2)/3)は、

-0.317338287203061937813337422441155649112826474209541704773596…

までは、グラフを確認して納得。ここで、次の値はどうやって計算したのですか？

-2.296520253118852045622163925693816744412216672265184546034003…


　らすかるさんからのコメントです。（平成２４年８月２５日付け）

　W(a)の値は、

(1)　aからW(a)の漸化式に使う初期値を計算する

　aの値によって（0、0に近い値、-1/eに近い値、その他）、また分岐によって処理方法や計
算式が異なります。

(2) 12次収束の漸化式を2回または3回計算する（180桁〜2200桁の場合）

という手順で計算しています。どちらの値の計算でも(2)の計算は全く同じで、(1)で計算する
初期値が-0.317…と-2.296…のどちらに近いかによって収束先が異なります。

　この処理の中身や計算式を書くことは出来なくはないですが、計算手順は高速化のため
に多くの場合分けをしており、また計算式も自作電卓用に最適化されていますので、書くと
とても長くなり、これをそのまま他の環境に移植してもあまり意味がありません。もし自分で
計算してみたいということであれば、環境（求めたい定義域、求めたい桁数、高速化が必要
かどうかなど）を教えていただければ、手頃な式を提示します。


　ＧＡＩさんからのコメントです。（平成２４年８月２５日付け）

　ｘ^ｘ^ｘ^ｘ.....=((ｘ^ｘ)^ｘ)^ｘ.....が収束するとき、ランベルト関数Ｗを用いて、Ｗ(-log(x))/(-log(x))
の極限値を持つ。

　これから、

(π/3)^(π/3)^(π/3)^(π/3)^.....=1.0495954675...

(π/4)^(π/4)^(π/4)^(π/4)^.....=0.8202519485...

(2^(1/2))^(2^(1/2))^(2^(1/2))^(2^(1/2))^.....=2

(2^(1/3))^(2^(1/3))^(2^(1/3))^(2^(1/3))^.....=1.3734671196...

(2^(1/4))^(2^(1/4))^(2^(1/4))^(2^(1/4))^.....=1.2396277295...

(2^(1/5))^(2^(1/5))^(2^(1/5))^(2^(1/5))^.....=1.1772785503...

なる関係が成立する。本日始めて知った知識なので、どなたか数値のチェックをして下さい。


　らすかるさんからのコメントです。（平成２４年８月２５日付け）

　((ｘ^ｘ)^ｘ)^ｘ.....　は、ｘ＞1のとき収束しません。ｘ^(ｘ^(ｘ^(ｘ^(ｘ^… ならば、値は正しいです。

ａ^ｘ=ｘ の解が、 ｘ=W(-loga)/(-loga) ですから、そのようになりますね。

　また、ちょっと気になったので、収束する条件を調べてみたのですが、ここにも

　　　分岐-1　（W(ｘ)＜-1である方）

の値が出てきました。W(ｘ)のうち分岐0の値をW₀(ｘ)、分岐-1の値をW₁(ｘ)として

　ｘ＞0、 a[n+1]=ｘ^a[n]　、 a[0]＞0 とするとき

　　　ｘ＜1 ならば、 a[0] の値にかかわらず 　W₀(-logｘ)/(-logｘ) に収束する

　　　ｘ＝1 ならば、 a[0] の値にかかわらず 1 に収束する

　　　ｘ＞e^(1/e)　(e^(1/e)≒1.444667861) ならば、 a[0]の値にかかわらず発散する

　　　1＜ｘ≦e^(1/e) のときは、

　　　　　　a[0]＞W₁(-logｘ)/(-logｘ) ならば、発散

　　　　　　a[0]＝W₁(-logｘ)/(-logｘ) ならば、 W₁(-logｘ)/(-logｘ) に収束

　　　　　　a[0]＜W₁(-logｘ)/(-logｘ) ならば、 W₀(-logｘ)/(-logｘ) に収束

となるようです。


　当ＨＰがいつもお世話になっているＨＮ「ＧＡＩ」さんからの問題提起です。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２６年９月３０日付け）

　e^ｘ＝ｘ　を満たす実数ｘは存在しない。そこで、　e^z＝ｚ を満たす複素数 ｚ を求めて下さい。


　Ｓ（Ｈ）さんから参考資料を頂きました。（平成２６年９月３０日付け）

　（参考）　Ｓ（Ｈ）さんの投稿


　らすかるさんからのコメントです。（平成２６年９月３０日付け）

　e^z＝ｚ より、　１＝ｚe^-z　すなわち、　−１＝−ｚe^-z

　よって、　−ｚ＝W(−１)　（ランベルトのW関数）　より、　ｚ＝−W(−１)　となり、初等関数
で解を書き表すことができません。

　数値的には、　ｚ＝ａ＋ｂ・ｉ　とおくと、　ａ＝ｅ^ａ・ｃｏｓｂ　、ｂ＝ｅ^ａ・ｓｉｎｂ

　ｂ＝ｅ^ａ・ｓｉｎｂ　から、　ａ＝log(ｂ/ｓｉｎｂ)　なので、　ａ＝ｅ^ａ・ｃｏｓｂ　から、

　　ｂ＝arccos(a/ｅ^ａ)＋２ｎπ＝arccos(log(b/sinb)/(b/sinb))＋２ｎπ

　よって、初期値を、(2n+1/2)π　として、　ｘ　←　arccos(log(ｘ/sinｘ)/(ｘ/sinｘ))＋２ｎπ
を繰り返すことで近似値が求められます。（適当な式なので収束は遅いです）

　求めたｘに対して、z=log(ｘ/sinｘ)±i・ｘ　が解となります。具体的には、

　n=0　のとき

z≒0.318131505204764135312654251588±1.337235701430689408901162143194i

　n=1　のとき

z≒2.062277729598283884978486720008±7.588631178472512622568923954108i

　n=2　のとき

z≒2.653191974038697286601106643318±13.949208334533214455288918039003i

　n=3　のとき

z≒3.020239708164501151377243687941±20.272457641615221810348855905451i

　　・・・・・・・・・・・・・・・・・・・

のようになります。