ガウス平面(今風に言えば、複素数平面)を用いると、複素数の四則演算の幾何学的意
味に気づかされる。現在の学習指導要領では、複素数平面を学習しないので、機械的な計
算はできても、その真実の意味を理解せずに終わってしまっている。非常に残念な数学教
程と言わざるをえない。
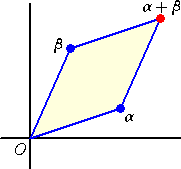
(1) 和 α+β ・・・ α、βが張る平行四辺形の第4頂点
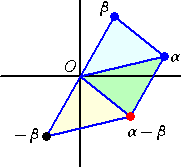
(2) 差 α−β ・・・ α、−βが張る平行四辺形の第4頂点
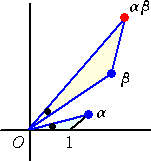
(3) 積 αβ ・・・ O1αに相似な三角形OβXの頂点X
|αβ|:|α|=|β|:1
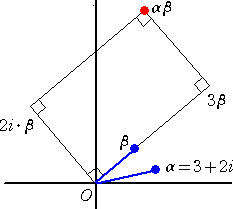
これについて、積 αβ の新しい視座を得た。例えば、
α=3+2・i 、βに対して、 αβ=3β+2・iβ と考える。
そうすれば、3βと2・iβの加法で簡単に積 αβ が求められ、三角形の相似の呪縛から
解放される。
理論的な展開には前者の方が優れていると思うが、実際に作図する場合は、後者の方が
勝ると思う。
