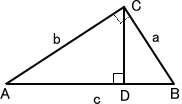
△ABC∽△CBD∽△ACD なので、
△ABC:△CBD:△ACD=c2:a2:b2 となる。
よって、c2=a2+b2 が成り立つ。(証終)
三平方の定理の証明は、100種類以上知られていると言われるが、次の証明の鮮やか
さは、多分ピカ一だろうと私的に思う。
 |
(証) △ABC=△CBD+△ACD において、 △ABC∽△CBD∽△ACD なので、 △ABC:△CBD:△ACD=c2:a2:b2 となる。 よって、c2=a2+b2 が成り立つ。(証終) |
因みに、この証明は、アインシュタインによるものらしい。
(追記) 今一緒に仕事をしている方から、三平方の定理の斬新な証明法を伺った。こちら
の方が、もしかしたらピカ一かもしれない。
上記の証明では、面積比は相似比の二乗に等しいという事実を用いている。因みに、こ
の事実は、現行の学習指導要領では、「数学 I 」で学ぶ事柄で、残念ながら中学校数学で
は扱われない。
伺った証明法では単に相似比を使い、しかも、「a2」等、普通面積と捉えられがちの所を
線分の長さとして捉えている点に、とても感動を覚えた。
(証)
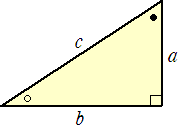 左図のような直角三角形において、相似な直角三角形
左図のような直角三角形において、相似な直角三角形
を2つ作り、等しい辺で貼り合わせて下図のような一つの
直角三角形を作る。
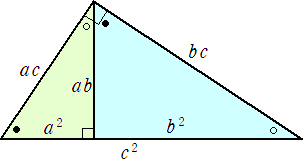
上図から、 c2=a2+b2 が成り立つことは明らかであろう。 (証終)
