・不思議な数６６・・・６　 　 　 　 　 　 　 　 　　　攻略法 氏

　１＋２＋３＋４＋５＋６＝２１

　１＋２＋３＋４＋５＋６＋・・・＋６４＋６５＋６６＝６６×６７/２＝２２１１

　　　・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

のように、

　1から「6がｎ個並んだ数」までの和は、

　　　　　　　　　　　　　「2がｎ個並んだ数」と「1がｎ個並んだ数」が並んだ数

となる。

（証明）　１がｎ個並ぶ数 11…1 を f(n) とすると、f(n)＝(10ⁿ-1)/９　と表せる。

　題意は、
　　　　　　　　
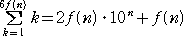
となる。

　左辺＝６f(n)（６f(n)＋１）/２

　　　 ＝f(n)（１８f(n)＋３）

　　　 ＝f(n)（１８・(10ⁿ-1)/９＋３）

　　　 ＝f(n)（２・(10ⁿ-1)＋３）

　　　 ＝２f(n)・10ⁿ＋f(n)

　　　 ＝右辺　　（証終）


（コメント）　計算のカラクリは、例えば、

　１＋２＋・・・＋６６６＝６６６×６６７/２＝３×６６７×１１１＝２００１×１１１＝２２２１１１

ですね！


　同様の現象が、偶数の場合も起こる。すなわち、

　２＋４＋６＝１２

　２＋４＋６＋・・・＋６４＋６６＝２（１＋２＋３＋・・・＋３３）＝３３×３４＝１１２２

　　　・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

のように、

　2から「6がｎ個並んだ数」までの偶数の和は、

　　　　　　　　　　　　　「1がｎ個並んだ数」と「2がｎ個並んだ数」が並んだ数

となる。

（証明）　題意は、
　　　　　　　　　　　　
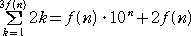
となる。

　左辺＝２・３f(n)（３f(n)＋１）/２

　　　 ＝f(n)（９f(n)＋３）

　　　 ＝f(n)（９・(10ⁿ-1)/９＋３）

　　　 ＝f(n)（10ⁿ−１＋３）

　　　 ＝f(n)・10ⁿ＋２f(n)

　　　 ＝右辺　　（証終）

　また、

　２＋４＋６＋８＋１０＋１２＝４２

　２＋４＋６＋・・・＋１３０＋１３２＝２（１＋２＋３＋・・・＋６６）＝６６×６７＝４４２２

　　　・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

のように、

　2から「6がｎ個並んだ数の２倍」までの偶数の和は、

　　　　　　　　　　　　　「4がｎ個並んだ数」と「2がｎ個並んだ数」が並んだ数

となる。

（証明）　題意は、
　　　　　　　　　　　　
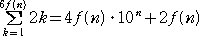
となる。

　左辺＝２・６f(n)（６f(n)＋１）/２

　　　 ＝f(n)（３６f(n)＋６）

　　　 ＝f(n)（３６・(10ⁿ-1)/９＋６）

　　　 ＝f(n)（４・10ⁿ＋２）

　　　 ＝４f(n)・10ⁿ＋２f(n)

　　　 ＝右辺　　（証終）


　ＦＮさんが、ｐ進法の問題に変えられました。（平成２３年７月２３日付け）

　1から「ａがｎ個並んだ数」までの和が、「ｂがｎ個並んだ数」と「ｃがｎ個並んだ数」を

並べた数に等しくなるという。これがすべての自然数ｎに対して成り立つための必要

十分条件を、ｐ、ａ、ｂ、ｃ の式で表せ。

　ただし、ｐ、ａ、ｂ、ｃ は整数で、0＜ａ、ｂ、ｃ＜ｐ とする。

　10進法(ｐ＝10)では、(ｐ，ａ，ｂ，ｃ)＝(10，6，2，1) 以外に解はありません。

　ｃ＝0 は認めてもいいのですが、一応除いています。

　ｃ＝0 を認めると、ｐが最小になる解は、(ｐ，ａ，ｂ，ｃ)＝(5，4，2，0)

　ｂ＝ｃ は認めることにしています。このとき、ｐが最小になる解は、(ｐ，ａ，ｂ，ｃ)＝(9，4，1，1)

　ｃ＞0 、 ｂ≠ｃ　とすると、ｐが最小になる解は、(ｐ，ａ，ｂ，ｃ)＝(10，6，2，1)


（コメント）　攻略法さんの手法を用いて、計算してみた。

　ｐ進数で、１がｎ個並ぶ数 11…1 を f(n) とすると、

　　　f(n)＝ｐ^ｎ-1＋ｐ^ｎ-2＋・・・＋ｐ＋１＝(ｐⁿ-1)/(ｐ-1)　と表せる。

　このとき、

　１＋２＋３＋・・・＋（ａｐ^ｎ-1＋ａｐ^ｎ-2＋・・・＋ａｐ＋ａ）

＝（ａｐ^ｎ-1＋ａｐ^ｎ-2＋・・・＋ａｐ＋ａ）（ａｐ^ｎ-1＋ａｐ^ｎ-2＋・・・＋ａｐ＋ａ＋１）/２

＝ａf(n)（ａf(n)＋１）/２

＝ａf(n)｛ａ(ｐⁿ-1)/(ｐ-1)＋１｝/２

＝｛ａ²/（２（ｐ−１））｝f(n)ｐⁿ＋｛（−ａ²＋ａｐ−ａ）/（２（ｐ−１）｝f(n)

＝ｂf(n)ｐⁿ＋ｃf(n)

となるためには、

　　ａ²/（２（ｐ−１））＝ｂ　すなわち　ａ²＝２ｂ（ｐ−１）　・・・　（*）

　（−ａ²＋ａｐ−ａ）/（２（ｐ−１）＝ｃ　すなわち、　−ａ²＋ａｐ−ａ＝２ｃ（ｐ−１）　・・・　（**）

　この（*）、（**）が求める必要十分条件かな？

　ここで、（*）、（**）を辺々加えて、両辺を ｐ−１ で割ると、　ａ＝２（ｂ＋ｃ）　が得られる。

　いま、ｐ＝10 とすると、（*）、（**）より、　ａ²＝１８ｂ　、　−ａ²＋９ａ＝１８ｃ

０＜ａ、ｂ、ｃ＜10　より、　ａ＝２（ｂ＋ｃ）≧４　なので、

　ａ²＝１８ｂ　を満たす整数の組 （ ａ ， ｂ ） は、　（ ａ ， ｂ ）＝（ ６ ， ２ ）　のみである。

　このとき、　ｃ＝１　となる。

　よって、　(ｐ，ａ，ｂ，ｃ)＝(10，6，2，1) 以外に解はない。


　ＦＮさんからのコメントです。（平成２３年７月２４日付け）

　正解です。式はできるだけ簡単な方がいいから１つ目と３つ目の方がいいと思います。

即ち、　ａ²＝２ｂ（ｐ−１）　、　ａ＝２（ｂ＋ｃ）

　式変形の最後の２式の両辺を、f(n)で割って、□ｐⁿ＋□＝□ｐⁿ＋□

ここで係数が等しいとするのは、ｐⁿ が異なる２つの値を取れば成り立つので問題はないの

ですが、恒等式という言葉は使えないので、私は、ｎ＝1、2 で成り立つことから２式を出し、

それが十分条件であることを確認しました。必要条件でしぼって、それが十分条件であるこ

とを確認するという書き方はごく普通のことで、入試とかにおいて、そのことを明示して「これ

は必要条件。十分条件であることを確認する」のように書くのは採点者の心証を良くする効

果があると思います。よくわからないで真似をすると心証を大きく悪くしますが。

　ａ²＝２ｂ（ｐ−１）　、ａ＝２（ｂ＋ｃ）　、０＜ａ、ｂ、ｃ＜ｐ　の整数解を求めておきます。

　第２式を第１式に代入して、２で割って、　２（ｂ²＋２ｂｃ＋ｃ²）＝ｂ（ｐ−１）

　ｂで割って、　２ｂ＋４ｃ＋２ｃ²/ｂ＝ｐ−１　より、　ｐ＝２ｂ＋４ｃ＋１＋２ｃ²/ｂ

　ここで、ｐが整数であることより、２ｃ²はｂで割り切れる。

　ｂ、ｃ が正の整数で、２ｃ²がｂで割り切れるとき、

　　　　　ａ＝２（ｂ＋ｃ）　、ｐ＝２ｂ＋４ｃ＋１＋２ｃ²/ｂ

とすれば、これは、　ａ²＝２ｂ（ｐ−１）　、ａ＝２（ｂ＋ｃ）　、０＜ａ、ｂ、ｃ＜ｐ　をみたす。

　従って、これが解である。

例　（ ｂ ， ｃ ）＝（ ２ ， １ ）　のとき、　（ ｐ ， ａ ）＝（ １０ ， ６ ）

　攻略法さんの２番目の式も一般化しておきます。(３番目は１番目を２倍したもの)

　ｐ進法で考える。

　2から「ａがｎ個並んだ数」までの偶数の和は、「ｂがｎ個並んだ数」と「ｃがｎ個並んだ

数」が並んだ数に等しくなるという。これがすべての自然数ｎに対して成り立つための

必要十分条件を、ｐ、ａ、ｂ、ｃ の式で表せ。

　ただし、ｐ、ａ、ｂ、ｃ は整数で、0＜ａ、ｂ、ｃ＜ｐ 、ａは偶数とする。

　ほとんど同様にできます。

　　ａ²＝４ｂ（ｐ−１）　、ａ＝２（ｂ＋ｃ）　になります。


　不思議な数「６６・・・６」に関連して、ペンネーム「数々の和」さんから、次のような性質があ
ることをご教示いただいた。（平成２３年７月２４日付け）

　56 は 7の倍数で、　56＝7×8
　6566 は 67の倍数で、　6566＝67×98
　665666 は 667の倍数で、　665666＝667×998
　66656666 は 6667の倍数で、　66656666＝6667×9998
　6666566666 は 66667の倍数で、　6666566666＝66667×99998
　　・・・・・・・・・・・・・・・・・・

（コメント）　例えば、

　　　　６５６６＝６７００−１３４

　　　　　　　　＝６７×１００−６７×２

　　　　　　　　＝６７×９８

　同様に、

　　　　６６５６６６＝６６７０００−１３３４

　　　　　　　　　　＝６６７×１０００−６６７×２

　　　　　　　　　　＝６６７×９９８

　　　・・・・・・・・・・・・・・・・・・・・・・・・・・・・

　とても面白い性質ですね！１３４と６７、１３３４と６６７、・・・　の関係が絶妙です．．．。


　ＦＮさんが、上記と似たようなことが起きるかどうか調べられました。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２３年７月２５日付け）

　似たようなことをどのようにとるかが問題ですが、次のようにしました。

「同じ数をn-1個並べて最後が1大きい数」×「9をn-1個並べて最後が異なる数」

＝「2n桁の数で1個を除いてすべて同じ数である数」

　ｐ進法であれば、9は、p-1に変わります。上記の条件を満たすものをすべて求めるのは
難しそうです。いくらかを求めることにします。一応、ｐ進法で考えますが、途中から10進法
にします。

　ｐ進法で考える。

　1をｎ個並べた数をA、1を２ｎ個並べた数をBとおく。すなわち、B＝Aｐⁿ＋A

A＝111･･･1＝1＋ｐ＋ｐ²＋･･･＋ｐ^n-1＝(ｐⁿ−1)/(ｐ−1)　より、  A(ｐ−1)＝ｐⁿ−1

同じ数をｎ-1個並べて、最後が1大きい数は、ａA＋1と書ける。

p-1をn-1個並べて、最後が異なる数は、ｐⁿ−ｂ＋1と書ける。
(ｐ-1がn-1個並び、最後がｂだとすると、ｐⁿ−ｐ＋ｂとなるので、最後の数を ｐ-b+1にした)

このとき、

(ａA＋1)(ｐⁿ−ｂ＋1)＝ａAｐⁿ−ａｂA＋ａA＋ｐⁿ−ｂ＋1

　　　　　　　　　　　　＝ａ(Aｐⁿ＋A)＋ｐⁿ−ａｂA−ｂ＋１

　ａ(Aｐⁿ＋A)＝ａB　であるから、ｐⁿ−ａｂA−ｂ＋１が ｐ^k・m の形でなければならない。

常識的に考えると、ｋは、ｎか0である。(論理的には甘いが多分正しい？)

ｐ^k・m の形であることは必要条件であって十分条件ではない。

　ｐⁿ−ａｂA−ｂ＋１＝ｐⁿ−ａｂ(ｐⁿ−1)/(ｐ−1)−ｂ＋１

ここで、ｋ＝0 とすると、ａｂ/(ｐ-1)＝１　より、 ａｂ＝ｐ-1　で、ａB−b＋2となる。

　これが条件を満たすためには、0≦ａ−ｂ＋２＜ｐで、

　　 (ａ，ｂ)＝(１，ｐ-1)は、ｐ≦4のとき条件を満たす。

　　 (ａ，ｂ)＝(ｐ-1，1)は、条件を満たさない。

　ここで、ｐ＝10とするとき、このどちらも解でない。

(ａ，ｂ)＝(3，3)　のとき、　333･･･34×999･･･98＝333333･･･32　である。

ここで、ｋ＝ｎ とする。ａｂは、ｐ-1で割り切れなければならないので、ａｂ＝(ｐ-1)cとおく。

これを代入すると、(1-c)ｐⁿ＋c−b＋1となるから、c＝b-1  、ａｂ＝(ｐ-1)(ｂ-1)

bとb-1は互いに素だから、ｂはｐ-1で割り切れる。ｂをｐ-1の約数として、ｐ-1＝ｂｄ　とおく。

　このとき、　ａ＝(ｂ-1)d　となる。

ｂ＝１のとき、ａ＝0となるから不適。

ｐ＝10とする。ｂ＝3、9　んとき、それぞれ　ａ＝6、8　となる。

　　　666･･･67×999･･･98＝666･･･65666･･･6

　　　888･･･89×999･･･92＝888･･･81888･･･8

10進法では、次のものがあることが確認できた。多分これ以外はない。

　　　　56＝7×8　　　　　　　　　18＝9×2　　　　　　　　　32＝4×8
　　　6566＝67×98　　　　　　　8188＝89×92　　　　　　　3332＝34×98
　　665666＝667×998　　　　　881888＝889×992　　　　　333332＝334×998
　66656666＝6667×9998　　　88818888＝8889×9992　　　33333332＝3334×9998
6666566666＝66667×99998　8888188888＝88889×99992　3333333332＝33334×99998


「同じ数をn-1個並べて最後が1大きい数」×「9をn-1個並べて最後が異なる数」

＝「2n桁の数で1個を除いてすべて同じ数である数」

　ＦＮさんが、このことを、もっと広げて次の形にして考察された。（平成２３年７月２６日付け）


「ｎ桁の数で1個を除いてすべて同じ数」×「ｎ桁の数で1個を除いてすべて同じ数」

＝「2n桁の数で1個を除いてすべて同じ数である数」

　これを理論的に扱うのは難しいので、Excel VBAで調べました。もちろんすべてのｎについ
て成り立つものを求めるので、特定のｎについても当然成り立つから、ｎ＝4として調べまし
た。結果は、8個ありました。

　　　3334×4999＝16666666   1
　　　3334×9998＝33333332   2 **
　　　4445×7999＝35555555   3
　　　5556×7999＝44442444   4
　　　6667×9998＝66656666   5 *
　　　6668×4999＝33333332   6
　　　6668×9998＝66666664   7
　　　8889×9992＝88818888   8 **

　これらはどれも4桁だけではなく何桁でも成り立ちます。*が当初の式、**が前に書いた式
です。1の一方または両方を2倍した式が、2、6、7です。


　ＦＮさん、ありがとうございます。私も、いくつか調べてみました。

　8889×9992＝88818888型

ｐ≧４　のとき、　(p-2)…(p-2)(p-1)×(p-1)…(p-1)2＝(p-2)…(p-2)1(p-2)…(p-2)

　2000×5000＝10000000型

ｐ＝ｘｙ≧４　のとき、　x0…0×y0…0＝10…0