・折り目の長さ　 　　 　　　　　　　　　　　　　　　　　Ｓ．Ｈ氏

　縦の長さが ａ 、横の長さが ｂ の紙（ａ＜ｂ）がある。

　　　　

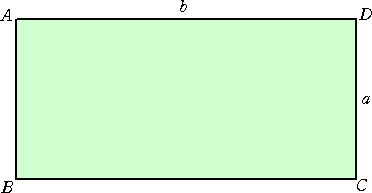
　この紙の頂点Ｂが辺ＡＤ上（頂点Ａは除く）にくるように紙を折り曲げる。

　　　　

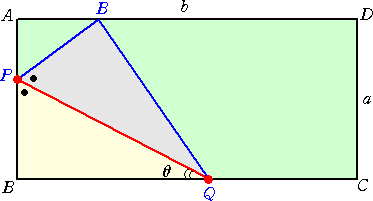
　このとき、折り目の長さには、どのような数理が秘められているのだろうか？少し気になっ
たので考えてみた。

　上図のように折り目がついているとき、 ∠ＰＱＢ＝θ　として、折り目ＰＱ（＝ ｘ ）の長さを
θ の関数として表してみよう。

　ＰＢ＝ｘ・ｓｉｎθ　で、　∠ＡＰＢ＝１８０°−２（９０°−θ）＝２θ　より、

　　　ＡＰ＝ＰＢ・ｃｏｓ２θ＝ｘ・ｓｉｎθ・ｃｏｓ２θ

となる。　ＡＰ＋ＰＢ＝ａ　なので、　　ｘ・ｓｉｎθ・ｃｏｓ２θ＋ｘ・ｓｉｎθ＝ａ

　よって、　ｘ＝ａ/｛ｓｉｎθ（１＋ｃｏｓ２θ）｝＝ａ/（２ｓｉｎθｃｏｓ²θ）＝ａ/（ｓｉｎ２θｃｏｓθ）

と書ける。

　しかし、折り目というと、上図のような場合以外に次のような場合も起こりうることに注意し
なければならない。その場合の折り目の長さを求めてみよう。

　　　　

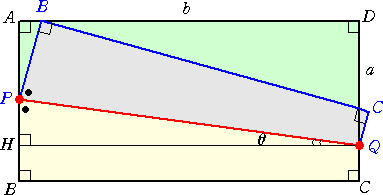
　上図の場合の折り目の長さは、明らかに、　ＰＱ＝ｂ/ｃｏｓθ　である。

この場合は、　ｓｉｎ２θ＜ａ/ｂ　の場合に起こる。


　　　　

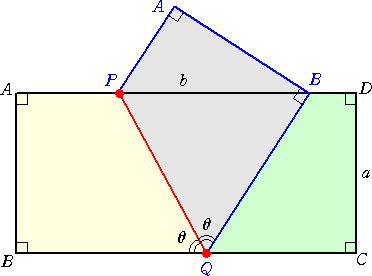
　上図の場合の折り目の長さは、明らかに、　ＰＱ＝ａ/ｓｉｎθ　である。

この場合は、　θ＞４５°の場合に起こる。




　　以下、工事中