私的数学塾の訪問者カウンタが、333333を通過したということで、次の計算式を思い
出した。
3×4=12
33×34=1122
333×334=111222
3333×3334=11112222
33333×33334=1111122222
・・・・・・・・・・・・・・・・・・・・・
この計算式の原理は、例えば、
333×334=111×3×(333+1)
=111×(999+3)
=111×(1000+2)
=111000+222
=111222
から、明らかだろう。
(コメント) とても面白い計算ですね!
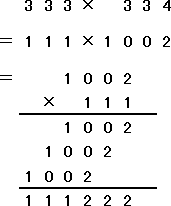
と計算してもいいのかな...。
Seiichi Manyamaさんからのコメントです。(平成28年3月27日付け)
上記を見て、真似してみました。
3×7=21
33×67=2211
333×667=222111
3333×6667=22221111
33333×66667=2222211111
・・・・・・・・・・・・・・・・・・・・・
この計算式の原理は、例えば、
33333×66667=11111×200001=2222211111 から、明らか。
さらに同じ理屈で次が言える。
132=3×44
113322=33×3434
111333222=333×334334
111133332222=3333×33343334
・・・・・・・・・・・・・・・・・・・・・
231=3×77
223311=33×6767
222333111=333×667667
222233331111=3333×66676667
・・・・・・・・・・・・・・・・・・・・・
1332=3×444
11333322=33×343434
111333333222=333×334334334
・・・・・・・・・・・・・・・・・・・・・
2331=3×777
22333311=33×676767
222333333111=333×667667667
・・・・・・・・・・・・・・・・・・・・・
一般化するとこんな感じか?
1 がm 個, 3 がm(n - 1) 個, 2 がm 個= (3 がm 個) x (「3 がm - 1 個に4」がn 個)
2 がm 個, 3 がm(n - 1) 個, 1 がm 個= (3 がm 個) x (「6 がm - 1 個に7」がn 個)
<前者のからくり>
1 がm 個, 3 がm(n - 1) 個, 2 がm 個
= (1 がm 個) x (1 の後に0 がm - 1 個, 「3 の後に0がm - 1 個」がn - 1 個, 2 が1 個)
= (1 がm 個) x 3 x (「3 がm - 1 個に4」がn 個)
= (3 がm 個) x (「3 がm - 1 個に4」がn 個)
<後者のからくり>
2 がm 個, 3 がm(n - 1) 個, 1 がm 個
= (1 がm 個) x (2 の後に0 がm - 1 個, 「3 の後に0がm - 1 個」がn - 1 個, 1 が1 個)
= (1 がm 個) x 3 x (「6 がm - 1 個に7」がn 個)
= (3 がm 個) x (「6 がm - 1 個に7」がn 個)
一般化ができていないが、上記の二つは次のようにして結び付けられる。
位の1つに、3 を足すと一つずれる
11112222 = 3333 x 3334
↓
11122221 = 3333 x 3337
↓
11222211 = 3333 x 3367
↓
12222111 = 3333 x 3667
↓
22221111 = 3333 x 6667
Seiichi Manyamaさんからのコメントです。(平成28年3月28日付け)
3が1と2に挟まると少し複雑になってきている。(→ 参考)
3を挟まなければ簡単なのだが…。(→ 参考) やっとわかりました。3を挟んでずらすの
ではなく、ずらしたものの真ん中に3を挟むことに!(→ 参考 ・・・ 修正)
親玉と子分3匹
Seiichi Manyamaさんからのコメントです。(平成28年3月29日付け)
こんなのもある。(→ 参考) さらにこんなのもある。(→ 参考)
いろいろ発見してきましたが、これまでの全パターンは、(Ruby)コードで網羅されます。
仕事から帰ってきて昨日のからくりについて考えていたら、簡単な理屈だった。具体例で
33…の商を作る方法を説明したらわかり易そうなので、もうしばらくお待ちください。
Seiichi Manyamaさんからのコメントです。(平成28年3月30日付け)
(→ 参考)
Seiichi Manyamaさんからのコメントです。(平成28年3月31日付け)
気に入った形(→ 参考) その他(→ 参考)
Seiichi Manyamaさんからのコメントです。(令和元年8月31日付け)
上記で、
3×7=21
33×67=2211
333×667=222111
3333×6667=22221111
33333×66667=2222211111
・・・・・・・・・・・・・・・・・・・・・
を報告したが、
33333 = 66666/2 、66667 = 66666+1
のような変形をすることで、
1+2+・・・+6 = 21
1+2+・・・+66 = 2211
・・・・・
1+2+・・・+66666 = 2222211111
のような変形も可能。(→ 参考:「A213516」)
