角の3等分に関わる問題で、次のような問題を最近経験した。
△ABCの辺BCの中点D、DCの中点Eに対して、線分AD、AEは∠Aの3等分線
であるものとする。BC=4 のとき、AEの長さを求めよ。
この問題を初めて見たとき、AB、ACの長さが与えられていないのに、「求まるの?」と
いう疑念が湧いたが、解いていくうちに、それが杞憂であることを悟らされた。
息子にこの問題を見せたら、彼は次のような図を書いてあっさり解いてしまった。
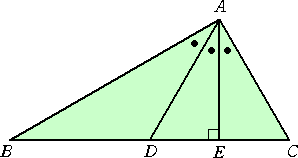
(解) 題意より、 BD=2 、 DE=EC=1 である。
ADは∠BAEの2等分線なので、 AB : AE=BD : DE=2 : 1 が成り立つ。
よって、 AE=m とおくと、 AB=2m とおける。
同様に、AEは∠DACの2等分線なので、 AD : AC=DE : EC=1 : 1 が成り立つ。
よって、 AD=AC より、△ADCは2等辺三角形となる。
EはDCの中点なので、 AE⊥DC すなわち、 ∠AED=90° となる。
このとき、△ABEは∠AED=90°の直角三角形となり、三平方の定理より、
(2m)2=32+m2
よって、 4m2=9+m2 より、 m2=3 から、 AE=m=
これに対して、当初私が想定した解答は下記のようなものである。
(解) ADは∠BAEの2等分線なので、 AB : AE=BD : DE=2 : 1 が成り立つ。
よって、 AE=m とおくと、 AB=2m とおける。
同様に、AEは∠DACの2等分線なので、 AD : AC=DE : EC=1 : 1 が成り立つ。
よって、 AD=AC=n とおける。
△ABCにおいて、中線定理より、 (2m)2+n2=2(n2+22) なので、
4m2−n2=8
同様に、 △ADCにおいて、中線定理より、 n2+n2=2(m2+12) なので、
n2−m2=1
よって、これらの連立方程式より、 3m2=9 から m2=3
したがって、 AE=m=
(コメント) いろいろな解法が楽しめる問題って、やはり面白いですね!
