・　正方形の面積（２） 　　　　　　　　　　　　　　　Ｓ．Ｈ氏

　以前、あるクイズ番組で、正方形の面積を問う問題が出題された。この問題を一般化し
て、下記のように解いてみた。

　１辺の長さが ａ＋１ の正方形ＡＢＣＤにおいて、各辺上に、

　　ＡＰ＝１　、ＢＱ＝１　、　ＣＲ＝１　、　ＤＳ＝１

となるように点 Ｐ、Ｑ、Ｒ、Ｓ をとる。

　このとき、線分 ＡＲ、ＢＳ、ＣＰ、ＤＱ で囲まれる正方形ＫＬＭＮの面積を求めよ。

　　　　　　　　　

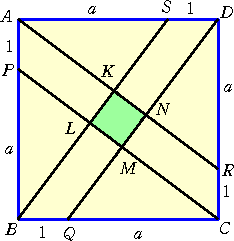
（解）　∠ＢＡＲ＝θ　とおくと、　ｔａｎθ＝（ａ＋１）/ａ　なので、

　　　　　　　

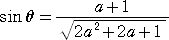
よって、正方形ＫＬＭＮの一辺の長さは、

　　　　　　　　

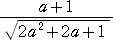
なので、正方形の面積 Ｓ は、

　　　　　　　　

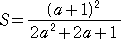
で与えられる。

　ここで、
　　　　　　　ａ＝１　（Ｐ、Ｑ、Ｒ、Ｓが各辺の中点）のとき、　Ｓ＝４/５

　　　　　　　ａ＝２　のとき、　Ｓ＝９/１３

　　　　　　　ａ＝３　のとき、　Ｓ＝１６/２５

　　　　　　　ａ＝４　のとき、　Ｓ＝２５/４１

　　　　　　　　・・・・・・・・・・・・・・・・・・

　クイズ番組は、「ａ＝２」の場合でした！

　クイズになるくらいだから、もしかしたら「グッ」とくる名答があるかも．．．。

　もっと初等的に求める方法を思いつかれた方、こちらまで是非ご教示下さい。

（追記）　平成２０年１１月２９日付け

　４人の方から、次のような別解を頂いた。別解をお寄せいただいた方に感謝します。

（らすかるさんの別解）
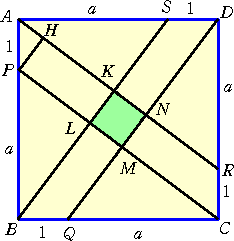　　　線分ＡＲに垂線ＰＨを引く。このとき、

　　　　　　△ＰＡＨ∽△ＢＳＡ　なので、

　　　ＰＨ²＝（ＰＨ/ＰＡ）²＝ＡＢ²/ＢＳ²

　　　よって、正方形の面積は、

　　　　　　





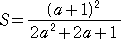
（コメント）　ＰＨ＝ＰＨ/ＰＡ　という発想が斬新ですね！

（ｅｉｂｕ さんの別解）
　　　左図において、ＫＮ＝ｘ、ＡＫ＝ＮＤ＝ｙ　とおくと、

　　ＫＳ‖ＮＤ　なので、ＡＫ ： ＫＮ＝ＡＳ ： ＳＤ＝ａ ： １

　　　すなわち、　ｙ ： ｘ＝ａ ： １　より　ｙ＝ａｘ

　　　一方、△ＡＮＤは直角三角形なので、

　　　　（ｘ＋ｙ）²＋ｙ²＝（ａ＋１）²

　　ｙ＝ａｘ　を代入して、
　　　　　　　　　　　　　　


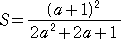
（コメント）　やはり、この問題で、「ｓｉｎ」を持ち出すのは、邪道ですかね？お二方の解答は
　　　　　　十分中学生にも分かる解答だと思います。

（高校３年　蕪昧さんの別解）

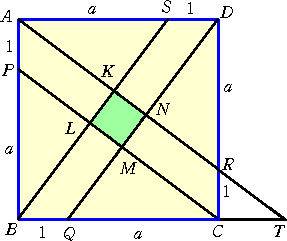ＡＲの延長線とＢＣの延長線の交点をＴとする。 　　ＤＲ：ＣＲ＝ａ：１　より、ＡＤ：ＣＴ＝ａ：１ 　　ＡＤ＝ａ＋１　なので、ＣＴ＝（ａ＋１）/ａ よって、　 　　ＱＴ＝（ａ2＋ａ＋１）/ａ　、ＢＴ＝（ａ＋１）2/ａ ここで、三平方の定理より、 　　ＡＴ2＝（ａ＋１）2（２ａ2＋２ａ＋１）/ａ2

　また、ＤＡ：ＱＴ＝ａ＋１：（ａ²＋ａ＋１）/ａ＝ａ²＋ａ：ａ²＋ａ＋１　より、

　　ＡＮ：ＴＮ＝ａ²＋ａ：ａ²＋ａ＋１

　ＡＮ＋ＴＮ＝ＡＴ　なので、

　　ＡＮ²＝（ａ²＋ａ）²/（２ａ²＋２ａ＋１）²×（ａ＋１）²（２ａ²＋２ａ＋１）/ａ²

　　　　　＝（ａ＋１）⁴/（２ａ²＋２ａ＋１）

　同様にして、　ＳＡ：ＢＴ＝ａ：（ａ＋１）²/ａ＝ａ²：（ａ＋１）²　より、 ＡＫ：ＴＫ＝ａ²：（ａ＋１）²

　ＡＫ＋ＴＫ＝ＡＴ　なので、

　　ＡＫ²＝ａ⁴/（２ａ²＋２ａ＋１）²×（ａ＋１）²（２ａ²＋２ａ＋１）/ａ²

　　　　　＝（ａ²＋ａ）²/（２ａ²＋２ａ＋１）

　ＫＮ＝ＡＮ−ＡＫ　より、正方形の一辺の長さが求められ、よって、

　　　　

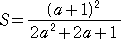
（コメント）　計算は十分中学生的ですが、少し計算がかかりすぎのような．．．予感。

（Ｏｘｉａさんの別解）
　　　三角形の相似より、ＡＫ：ＫＮ＝ＢＬ：ＬＫ＝ａ：１
　　なので、正方形ＫＬＭＮの一辺の長さを ｘ とおくと、

　　　　ＢＫ＝（ａ＋１）ｘ　、　ＡＫ＝ＢＬ＝ａｘ

　　また、正方形ＡＢＣＤの一辺の長さは、ａ＋１ より、
　　△ＢＡＫで三平方の定理より、

　　　　（ａ＋１）²ｘ²＋ａ²ｘ²＝（ａ＋１）²

　　　これより、
　　　　　　　　　


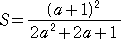
（コメント）　ｅｉｂｕさんの別解と趣旨は同じでした。

　まだ、「グッ」とくる名答に出会えていない．．．。確かクイズ番組では、もっと簡単に示して
いたような．．．思い出せない、残念！

（追記）　平成２０年１１月３０日付け

　さらに、多くの方から、次のような別解を頂いた。別解をお寄せいただいた方に感謝します。

（ｚｋ４３さんの別解）

２つの平行四辺形ＡＰＣＲ、ＢＱＤＳを取り去って、 　　１辺の長さ ａ の正方形にすると、やはり中に小さい 　　正方形ができる。この小さい正方形の面積は、 　　　　（ａ2/（ａ＋１）2）×Ｓ 　　よって、 　（ａ＋１）2−｛２（ａ＋１）−Ｓ｝＝ａ2−｛ａ2/（ａ＋１）2｝Ｓ 　　より、

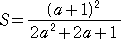（コメント）　三平方の定理を使うのは避けたい、平方根も使いたくない、・・・と贅沢なことを
　　　　　　考えていましたが、ｚｋ４３さんの別解で眼前の暗雲が雲散霧消しました。初等的
　　　　　　すぎるくらい初等的で感動しました。ただ惜しむらくは、面積比が相似比の２乗に
　　　　　　比例することを用いているので、高校１年レベルでしょうか？もっとも、この程度の
　　　　　　知識は、小学校レベルでも理解できないことはないと思いますが．．．。

（あとねこさんの別解）
　　蕪昧さんの別解の図から、

　　ＤＮ：ＮＭ：：ＭＱ＝ａ（ａ＋１）：ａ＋１：ａ²

　となり、簡単に正方形の１辺が求まる。



（コメント）　比の計算が難しい．．．予感。







（高校３年　Ｆさんの別解）

△ＤＭＣ∽と△ＤＣＱ で、相似比は、ＤＣ ： ＤＱ＝ａ＋１ ：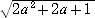

また、　２△ＤＱＣ＝□ＡＢＣＤ−平行四辺形ＢＱＤＳ＝ａ（ａ＋１）

求める面積 Ｓ は、□ＡＢＣＤから４△ＤＣＭ を引いたものに等しいので、

　Ｓ＝（ａ＋１）²−２ａ（ａ＋１）×（ａ＋１）²/（２ａ²＋２ａ＋１）　より、

　　　　

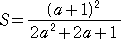
　ところで、質問です。

　□ＫＬＭＮの面積 → ０．５　（ａ → ∞）　と出てきますが、これは一体何を示しているので
しょうか？

（コメント）　Ｓの分母と分子は、「同位の無限大」という事実しかないように思います。
　　　　　　収束値が０でないことが重要で、「０．５」という数字に特段大きな意味はないもの
　　　　　　と思われます。

（ＧＡＩ さんの別解）

　　　ａ＝２　のとき、正方形ＫＬＭＮの各辺に平行な補助線（幅は正方形の一辺の長さ）を

　書き入れると、もとの正方形ABCDの中に正方形KLMNと同形とならない半端な図形が

　１６個できるが、この半端図形同士を組み合わせて、正方形KLMNと同形にできる。

　　　　　　　　　

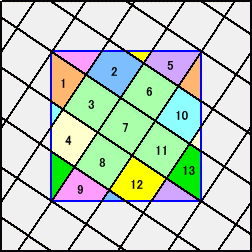
　　こうして結局、大きな正方形ＡＢＣＤの中には小さな正方形KLMNの形がぴったり１３個

　入る。従って、求める面積は、ａ＝２　のときは、　３×３÷１３＝９/１３

　こう考えると、

　　ａ＝３ では小さな正方形が、　１＋３＋５＋７＋５＋３＋１＝２５（個）　入る。

　　ａ＝４ では小さな正方形が、　１＋３＋５＋７＋９＋７＋５＋３＋１＝４１（個）　入る。

一般に、

　　１＋３＋５＋・・・＋（２ａ−１）＋（２ａ＋１）＋（２ａ−１）＋・・・＋５＋３＋１

　＝２×ａ²＋（２ａ＋１）＝２ａ²＋２ａ＋１（個）

の小さな正方形が、元の正方形ＡＢＣＤにぴったり含まれるので、一個あたりの面積は、

　　　　

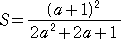
となる。

（コメント）　面白いユニークな解法ですね！正しく、これはクイズの答えらしい爽やかさに
　　　　　　溢れています．．．。　私が待ち望んだ解答です。ＧＡＩ さんに感謝！

（蕪昧さんの新しい別解）
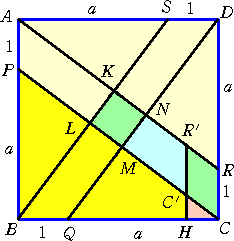　　　台形ＮＭＣＲを、「Ｎ→Ｋ」、「Ｍ→Ｌ」となるように平
　　行移動させる。

　　　点Ｃおよび点Ｒの移動先の点を、Ｃ’、Ｒ’とし、Ｃ’
　　からBCに下ろした垂線の足をＨとする。

　　　この時、ＣＣ’＝ＭＬである。

　　　また、正方形ＫＬＭＮと平行四辺形Ｒ’Ｃ’ＣＲの面
　　積は等しく、ＣＲ＝１　より、ＣＨ＝Ｓ　となる。

　　　　△ＰＢＣ∽△Ｃ’ＨＣ より、

　　　　　　ＰＣ² ： ＢＣ²＝Ｃ’Ｃ² ： ＨＣ²


　　　三平方の定理より、　ＰＣ²＝２ａ²＋２ａ＋１　なので、

　　　　　　２ａ²＋２ａ＋１ ： （ａ＋１）²＝Ｓ ： Ｓ²＝１ ： Ｓ

　　となり、これを解いて、
　　　　　　　　　　　　　　　　

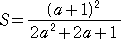
（コメント）　新しい別解を考えられた蕪昧さんに感謝。計算がスッキリしましたね！

　　　　　　平行移動した後の、線分ＣＣ’の長さが求める正方形の一辺の長さに等しいこと、
　　　　　線分ＣＨの値が丁度求める面積の値と等しいことを利用した解法で、数学に対する
　　　　　蕪昧さんの非凡さを感じさせます。

（追記）　平成２０年１２月４日付け

（ｚｋ４３さんの新しい別解）
　　　平行四辺形ＡＰＣＲの面積について、

　　　　　ＡＰ×ＡＤ＝ＡＲ×ＫＬ

　　　すなわち、

　　　　　１×（ａ＋１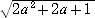）＝×ＫＬ

　　　これより、　Ｓ＝ＫＬ²は、

　　　　　　　　　



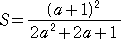
（コメント）　平行四辺形の面積を２通りに計算する手法に感動しました。



　この話題と同様な問題が灘中学入試（２００７）で出題された。



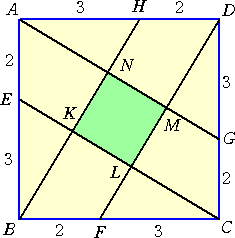
　　　左図の四角形ＡＢＣＤは、１辺５ｃｍの正方形で、

　　ＡＥ、ＢＦ、ＣＧ、ＤＨの長さはすべて２ｃｍである。

　　　斜線部分の面積を求めよ。








（解）
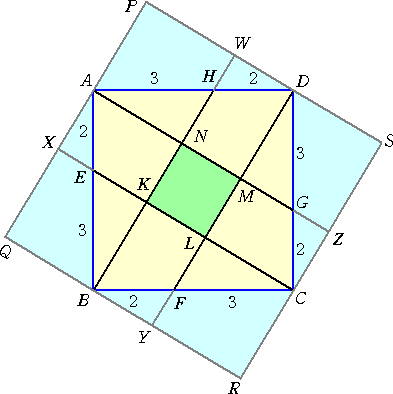△ＢＥＫ∽△ＢＡＮ　より、

△ＢＥＫ ： △ＢＡＮ
　＝３² ： ５²＝９ ： ２５　なので、

△ＢＥＫ ： □ＥＫＮＡ＝９ ： １６

　　ここで、

　　△ＡＢＨ＝３・５/２＝１５/２

なので、

（９＋１６＋９）ｋ＝１５/２　より、

　　　　ｋ＝１５/６８

よって、求める面積は、

２５−（９＋１６）ｋ・４

＝５０/１７　　（終）



　この問題については、いろいろな別解が考えられる。

（別解）　ＫＮ＝２ｍ　とおくと、　ＢＫ＝ＮＷ＝３ｍ　なので、

　　　　正方形ＡＢＣＤ ： 正方形ＫＬＭＮ

　　＝ （８ｍ）²−４・３ｍ（３ｍ＋２ｍ）/２ ： （２ｍ）² ＝ ３４ ： ４

　　したがって、　求める面積は、　２５×４/３４＝５０/１７　　（終）

（コメント）　何となく別解の方が小学生向きですね！


（別解）　ＫＮ＝２ｍ　とおくと、　ＢＫ＝３ｍ　なので、

　　　　　　　　　ＡＢ²＝（３ｍ＋２ｍ）²＋（３ｍ）²＝３４ｍ²＝２５

　　　　このとき、　ｍ²＝２５/３４　なので、求める面積は、　（２ｍ）²＝５０/１７　　（終）

（コメント）　この別解では、三平方の定理が用いられているので、中学生向きかな！

　数学セミナー（２００９年１月号　日本評論社）の「エレガントな解答をもとむ」でも、同様な
問題が取り上げられた。

　正方形の折り紙を折って面積が元の大きさの１/５となる正方形の一辺を作図せよ。

（解）　２²＋１²＝５　なので、
　　　　　　　　　　　　　　　　

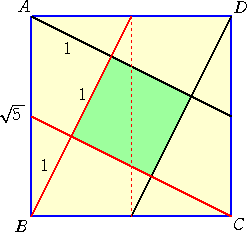
　したがって、折り紙を３回折れば、面積 １ の正方形の１辺の長さを見いだすことができる。


（追記）　平成２１年１０月２５日放送の「熱血！平成教育学院」（フジテレビ系）で同様の図
　　　　形を題材とする問題が出題された。次はその問題を改題したものである。



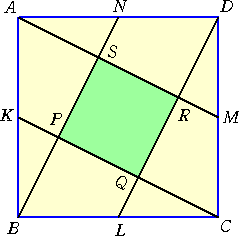
　　　左図のように、面積４５の正方形ＡＢＣＤの各辺の

　　中点をＫ、Ｌ、Ｍ、Ｎとし、これらと頂点を結んで、正

　　方形ＰＱＲＳを作る。このときできる正方形の一辺

　　の長さＰＱを求めよ。






　数学セミナーの問題のように考えれば、正方形ＰＱＲＳの面積は、　４５÷５＝９　となるの

で、明らかに、　ＰＱ＝３　となる。

　正方形ＰＱＲＳがもとの正方形ＡＢＣＤの１/５という感覚は、次の図と睨めっこをすると、自
然に了解されるだろう。