・　方べきの定理もどき 　 　 　 　 　 　　　　　　　Ｓ．Ｈ氏

　平成２０年度入試　学習院大学　理学部で次のような問題が出題された。

　放物線 Ｃ ： ｙ＝ｘ²＋ｂｘ＋ｃ は ｘ 軸と相異なる２点で交わるとし、その交点を左か

ら順に Ａ、Ｂ とする。ｘ 軸上でＢの右にある点Ｐ（ｔ，０）から、ＡとＢの間にあるＣの部

分に接線を引き、その接点をＱとする。Ｑから ｘ 軸に下ろした垂線の足をＲとすると

き、 ＲＰ²＝ＡＰ・ＢＰ　を証明せよ。

　多少計算に腕力があれば、強引に計算を進めて完答できる問題であるが、次のように解
けば、エレガントだろう。

（解）　Ａ（α，０）、Ｂ（β，０）　（α＜β）とすると、α、βは、２次方程式　ｘ²＋ｂｘ＋ｃ＝０

　　　の相異なる解である。解と係数の関係から、　α＋β＝−ｂ　、　αβ＝ｃ

　　　　このとき、　ＡＰ・ＢＰ＝（ｔ−α）（ｔ−β）＝ｔ²＋ｂｔ＋ｃ　となる。

　　　Ｑ（ｓ，ｓ²＋ｂｓ＋ｃ）における接線の方程式は、

　　　　　　　　ｙ＝（２ｓ＋ｂ）（ｘ−ｓ）＋ｓ²＋ｂｓ＋ｃ＝（２ｓ＋ｂ）ｘ−ｓ²＋ｃ

　　　これが、Ｐ（ｔ，０）を通るので、　（２ｓ＋ｂ）ｔ−ｓ²＋ｃ＝０　より、　ｓ²＝（２ｓ＋ｂ）ｔ＋ｃ

　　　このとき、　ＲＰ²＝（ｔ−ｓ）²＝ｔ²−２ｔｓ＋ｓ²＝ｔ²−２ｔｓ＋（２ｓ＋ｂ）ｔ＋ｃ＝ｔ²＋ｂｔ＋ｃ

　　　よって、　ＲＰ²＝ＡＰ・ＢＰ　が成り立つ。　（終）

　　　　　　　　　　

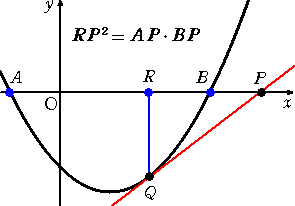
　この図を見ていると、何となく方べきの定理の「放物線」版かなと感じる。とても美しい性
質だ。

　それにしても、問題文に記述のある「交点」とか「垂線の足」という用語をみると、この問
題の作問者は、相当年配の方のような気配ですね！最近の教科書では、あまり用いない
言葉なもので．．．。