・ ある場合の数 S.H氏
2つの正の整数 A 、 B について、最大公約数を G とすると、
A=aG 、 B=bG ただし、 a と b は互いに素
と書かれることは、よく知られた事実である。また、このとき、最小公倍数 L は、
L=abG
で求められる。
最近、この公式を用いた問題で感動的な計算手法に遭遇したので紹介したいと思う。
問 題 2つの正の整数 A 、 B (A<B) の最小公倍数が、30 となるような
A 、 B の
組(A,B)は何通りあるか?
まずは、誰でも(?)が計算すると思われるような方法から...。
(解) 最大公約数を G とすると、 A=aG 、 B=bG (ただし、
a と b は互いに素)
と書ける。このとき、 abG=30=2×3×5 で、 2 、3 、5 は互いに素である。
最大公約数 G の取り得る値は、 G= 1 、 2 、 3 、 5 、 6 、
10 、 15 、 30 で、
場合に分けて数え上げる。
G=1 のとき、 ab=30=2×3×5 (ただし、 a と b
は互いに素)
このとき、 a = 1 、 2 、 3 、 5 、 6 、 10 、 15
、 30
b = 30 、 15 、 10 、6 、 5 、 3 、
2 、 1
A<B より、 a<b なので、
( a , b )=( 1 , 30 )、( 2 , 15 )、(
3 , 10 )、( 5 , 6 )
よって、このときの場合の数は、 4通り
G=2 のとき、 ab=15=3×5 (ただし、 a と b は互いに素)
このとき、 a = 1 、 3 、 5 、 15
b = 15 、 5 、 3 、 1
A<B より、 a<b なので、 ( a , b )=( 1
, 15 )、( 3 , 5 )
よって、このときの場合の数は、 2通り
G=3 、 5 のときも同様にして場合の数はそれぞれ、 2通り
G=6 のとき、 ab=5 (ただし、 a と b は互いに素)
このとき、 a = 1 、 5
b = 5 、 1
A<B より、 a<b なので、 ( a , b )=( 1
, 5 )
よって、このときの場合の数は、 1通り
G=10 、 15 のときも同様にして場合の数はそれぞれ、 1通り
G=30 のとき、 ab=1 (ただし、 a と b は互いに素)
このとき、 a = 1 で、 b = 1
これは、 A<B より、 a<b であることに矛盾する。
よって、このような場合は起こらない。
以上から、求める場合の数は、 4+2+2+2+1+1+1=13 (通り) (終)
これに対して、次のような解答を見せられると、暑さが吹っ飛ぶようだ。
(別解) 最大公約数を G とすると、 A=aG 、 B=bG (ただし、
a と b は互いに素)
と書ける。このとき、 abG=30=2×3×5 で、 2 、3 、5 は互いに素である。
2 という値は、 a または b または G の何れかが取り得る。よって、3 (通り)。
このうちの1通りに対して、
3 という値も、 a または b または G の何れかが取り得るので、3 (通り)。
このうちの1通りに対して、
5 という値も、 a または b または G の何れかが取り得るので、3 (通り)。
よって、 a 、 b 、 G の3個の文字の重複順列の数は、 33=27 (通り)
このうち、 GGG すなわち、 a=1、b=1、G=30 という場合は除かれる。
また、 A<B より、 a<b であるので、求める場合の数は、
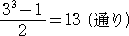 (終)
(終)
(コメント) 別解のような柔軟な発想に、いたく感動しました!
読者のために、練習問題を残しておくことにしよう。
練習問題 2つの正の整数 A 、 B (A<B)の最小公倍数が、210 となるような A 、B
の組(A,B)は何通りあるか?
(解) 210=2×3×5×7 より、求める場合の数は、(34−1)/2=40 (通り) (終)
この解法について、FNさんが研究の端緒を開かれた。(平成22年6月6日付け)
上記の問題を完全に一般的な形にするのは表現が複雑になるだけである。少し一般化
した次の問題が解ければこの手の問題はすべて解けることになる。
2つの正の整数A、B(A<B)の最小公倍数が 2p・3q・5r となるような組は何通
りあるか?
この問いかけに、GAI さんが表を活用して解を求められた。(平成22年6月7日付け)
| p |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
| q |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
2 |
2 |
2 |
| r |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
| 組の数 |
27 |
45 |
63 |
81 |
45 |
75 |
105 |
135 |
63 |
105 |
147 |
189 |
75 |
125 |
175 |
| p |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
| q |
2 |
3 |
3 |
3 |
3 |
4 |
4 |
4 |
4 |
1 |
1 |
1 |
1 |
| r |
4 |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
| 組の数 |
225 |
105 |
175 |
245 |
315 |
135 |
225 |
315 |
405 |
63 |
105 |
147 |
189 |
| p |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
| q |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
| r |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
| 組の数 |
105 |
175 |
245 |
315 |
147 |
245 |
343 |
441 |
この表から、2p・3q・51 の数列に注目すると、
| p |
1 |
1 |
1 |
2 |
2 |
2 |
3 |
3 |
3 |
| q |
1 |
2 |
3 |
2 |
3 |
4 |
1 |
2 |
3 |
| r |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 組の数 |
27 |
45 |
63 |
75 |
105 |
135 |
63 |
105 |
147 |
となっている。
p=1 のとき、q=1、2、3 と増えるに従い、組の数も 27、45、63 と増えている。
この数列は、初項 27 で、公差 18 の等差数列と考えられる。
同様に、
p=2 のとき、q=2、3、4 と増えるに従い、組の数も 75、105、135 と増えている。
このことから、q=1 も含めて、初項 45 で、公差 30 の等差数列と考えられる。
このとき、p=1 から p=2 と増えるに従い、 27 から 45 と 18 だけ増えている。
p=3 のとき、q=1、2、3 と増えるに従い、組の数も 63、105、147 と増えている。
この数列は、初項 63 で、公差 42 の等差数列と考えられる。
このとき、p=2 から p=3 と増えるに従い、 45 から 63 と 18 だけ増えている。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
以上から、 p=1、2、3 に対応する数列は、 27、45、63 なので、
一般項は、 27+18(p−1)=9(2p+1)
p=1、2、3 に従い、増える組の数は
q=1 のとき、 0 、 0 、 0
q=2 のとき、 18 、30 、 42
q=3 のとき、 36 、 60 、 84
よって、一般に、 2p・3q・51 となるような組は、
32(2p+1)+{18+12(p−1)}(q−1) ・・・(***)
であることが導かれ、 2p・3q・5r となるような組は、
(***)+[18+12(p−1)+{12+8(p−1)}(q−1)](r−1)
=(***)+{12p+6+(4+8p)(q−1)}(r−1)
で与えられるので、これを整理すると、
=(2p+1)(2q+1)(2r+1)
に辿り着きました。(意外と美しい式に終わりびっくり!)
A=B のときと B<A での対称形を考慮して、求める場合の数は、
{(2p+1)(2q+1)(2r+1)−1}/2
となる。
FNさんによれば、上記の式でOKとのこと!(平成22年6月7日付け)ただ式の導き方と
しては、「投稿一覧」の「ある場合の数」の解答とほとんど同じように、もっと直接的にできる
そうである。
下記の解はFNさんによるものである。(平成22年6月9日付け)
(解) A、Bの最大公約数をGとして、 A=aG 、B=bG (ただし、
a と b は互いに素)
とする。このとき、 abG=2p・3q・5r において、素因数2について考える。
a、b、G で素因数2を、合わせてp個持つが、a、bは互いに素だから、一方は素因数2
を持たない。bが素因数2を持たない場合を考えると、aとGで、合わせてp個持つことに
なり、
(aに含まれる2の個数,Gに含まれる2の個数)=(0,p)、(1,p−1)、・・・、(p,0)
の p+1通りある。このうち最初のもの以外は、a、b を入れ替えたものがあるので、合わ
せて、2p+1通りとなる。
このうちの1通りに対して、素因数3について同様にして、2q+1通り、さらに、このうち
の1通りに対して、素因数5について、2r+1通りある。
従って、積の法則により、求める場合の数は、(2p+1)(2q+1)(2r+1)通りとなる。
この中に、a=1、b=1、G=2p・3q・5r 即ち A=B の場合が入っているので、これは
除き、さらに、A<B なので、2で割って結果が得られる。(終)
(コメント) この解は、冒頭の問題の本解の方の流れを汲む解法ですね!
さらに、GAI
さんは、次のような新しい問題を提起された。(平成22年6月8日付け)
3つの正の整数A、B、C(A<B<C)の最小公倍数が 2p・3q・5r となるような
組は何通りあるか?
さらに、
4つの正の整数A、B、C、D(A<B<C<D)の最小公倍数が 2p・3q・5r とな
るような組は何通りあるか?
これに対して、FNさんは、素因数の数を減らし、A<B<Cという条件を無視して、次の問
題を提起された。(平成22年6月8日付け)
3つの正の整数A、B、Cの最小公倍数が 2p となるような組は何通りあるか?
この問題の解答として、GAI
さんは、「3p2+3p+1」であることを見いだされた。
(平成22年6月8日付け)
FNさんによれば、素因数が1個の場合を補題として独立させ、問題を2つに分ければ、も
っとすっきりするだろうとのことである。(平成22年6月9日付け)
補 題 p を素数、e を自然数とする。2つの自然数A、Bの最小公倍数が、pe と
なるようなA、Bの組は、2e+1通りある。
命 題 p、q、・・・、r を素数、e、f、・・・、g を自然数とする。
2つの自然数A、B(A<B)の最小公倍数が、pe・qf・・・rg となるような
A、Bの組は、 {(2e+1)(2f+1)・・・(2g+1)−1}/2 通りある。
上記において、補題部分すなわち素因数1個の場合がかなり重要な位置を占めています。
3つの整数A、B、C の場合でもそうです。当然2つの場合より難しいです。考え方は同様で
すが簡単な数列の和を計算することになります。ということで前に書いた問題
3つの正の整数A、B、Cの最小公倍数が 2p となるような組は何通りあるか?
あるいは
補 題 p を素数、e を自然数とする。3つの自然数A、B、Cの最小公倍数が、pe と
なるような組は、3e2+3e+1通りある。
の証明はどうなるでしょうか?
このFNさんの問いかけに対して、らすかるさんが補題を一般化して証明された。
(平成22年6月9日付け)
補 題(らすかる)
p を素数、e を自然数とする。n個の自然数の最小公倍数が、pe となるような組
は、(e+1)n−en 通りある。
(証明) n個の自然数がすべて p0〜pe のいずれかである場合の数 (e+1)n から
n個の自然数がすべて p0〜pe-1 のいずれかである場合の数 en を引けばよい。
(証終)
(コメント) 言われてみると思わず納得...。正に「目から鱗」の証明で感動しました!
平成22年6月14日付けで、FNさんより、GAIさんが提起された次の問題
3つの正の整数A、B、C(A<B<C)の最小公倍数が 2p・3q・5r となるような
組は何通りあるか?
の解答をお寄せいただいた。FNさんに感謝します。
次の補題は、3個を n 個にした形でらすかるさんが証明された。
補 題 p を素数、e
を自然数とする。3つの自然数A、B、Cの最小公倍数が、pe と
なるような組は、3e2+3e+1通りある。
補 題(らすかる)
p を素数、e
を自然数とする。n個の自然数の最小公倍数が、pe となるような組
は、(e+1)n−en
通りある。
文字の使い方が問題と補題で違うことに注意。補題及び2個の場合の結果(ただし、A<B
でなく、A≠Bとした形で書くことにする)
2つの正の整数
A、B(A≠B)の最小公倍数が、2p・3q・5r となるような組は、
(2p+1)(2q+1)(2r+1)−1
通りある。・・・(*)
を用いて解く。
(解) まず、条件 A<B<C がないとして考える。
正の整数 A、B、C の最小公倍数が、2p・3q・5r であるとする。もちろん、A、B、C は、
2、3、5以外の素因数を持たない。
Aを素因数分解したときの2の累乗部分を A1、3の累乗部分を A2、5の累乗部分を A3
とする。このとき、 A=A1・A2・A3 である。
(もちろん、A1、A2、A3
のどれか1つか2つ或いは全部が1であることはありうる。)
B、Cも同様に、B=B1・B2・B3、C=C1・C2・C3 とする。
A1、A2、A3
の最小公倍数は、2p であるから、A1、A2、A3
の取り方は、補題により
3p2+3p+1通りある。
同様にして、B1、B2、B3 の取り方、C1、C2、C3 の取り方もそれぞれ、
3q2+3q+1通り 、3r2+3r+1通り である。
従って、A、B、C の取り方は、( 3p2+3p+1)(3q2+3q+1)(3r2+3r+1)通りある。
この中には2つが同じ場合、3つが同じ場合も含む。
3つが同じ場合は1通りである。
2つが同じ場合を考える。
A=B≠C の場合は(*)と同じである。B=C≠A、C=A≠B についても同様。
従って、3(2p+1)(2q+1)(2r+1)−3 通りある。
以上から、A、B、C がすべて異なる場合は、
(
3p2+3p+1)(3q2+3q+1)(3r2+3r+1)
−{3(2p+1)(2q+1)(2r+1)−3}−1通り
すなわち、
(
3p2+3p+1)(3q2+3q+1)(3r2+3r+1)−3(2p+1)(2q+1)(2r+1)+2通り
このうち、A<B<C となるのは、1/6なので、求める場合の数は、
{(
3p2+3p+1)(3q2+3q+1)(3r2+3r+1)
−3(2p+1)(2q+1)(2r+1)+2}/6 通り
となる。 (終)
さらに、FNさんは、これを 4個、5個、・・・としたときに、できそうかどうかを考えられた。
2つのとき、A<B、3つのとき、A<B<C としたが、上の証明でもわかるように、A と B
あるいは、A と B と C は相異なる、とする方が自然である。後で、2!や3!、・・・、n!で
割るかどうかだけのことなので問題として、次の形で考える。
相異なる n 個の自然数でその最小公倍数が、
L=pe・qf・・・・rg (p、q、・・・r
は相異なる素数、e、f、・・・g
は自然数)
であるような組は何通りあるか。
この答えを、F(n)通りと書くことにする。
まず、らすかるさんの一般化された補題:
補 題(らすかる)
p を素数、e
を自然数とする。n個の自然数の最小公倍数が、pe となるような組
は、(e+1)n−en
通りある。
において、 (e+1)n−en=w(n,e) と書くことにする。
まず、相異なるという条件を忘れて、最小公倍数が L=pe・qf・・・・rg であるような n 個
の自然数の組が、「w(n,e)w(n,f)・・・w(n,g)通り」あることは上と同様に考えてわかる。
L=pe・qf・・・・rg は固定して考えるので、w(n,e)w(n,f)・・・w(n,g)=W(n)と書くこと
にする。
このとき、先の結果より、
W(1)=1 、 W(2)=(2e+1)(2f+1)・・・(2g+1)
W(3)=(3e2+3e+1)(3f2+3f+1)・・・(3g2+3g+1)・・・
である。
上で示したことは、 F(3)=W(3)−3W(2)+2W(1) である。
また、2個、1個の場合の結果は、F(2)=W(2)−W(1)、F(1)=W(1) である。
F(3)を計算した過程を書けば、
F(3)=W(3)−3F(2)−F(1)
=W(3)−3(W(2)−W(1))−W(1)
=W(3)−3W(2)+2W(1)
そこで、4個の場合を考えると、
F(4)=W(4)−6F(3)−(4+3)F(2)−F(1)
=・・・・
=W(4)−6W(3)+11W(2)−6W(1)
ただし、6F(3)の6は、4C2 で、(4+3)F(2)の4は、4C1 で、3は、4C2/2 である。
(コメント) 考え方の道筋が分かりました。FNさんに感謝します。
以下、工事中

